leetcode刷题记录,有关树的简单难度算法题
530. 二叉搜索树的最小绝对差
题目:给你一棵所有节点为非负值的二叉搜索树,请你计算树中任意两节点的差的绝对值的最小值。

通过中序遍历二叉搜索树得到的关键码序列是一个递增序列。
中序遍历二叉搜索树,第一个结点外的每个节点与其前一节点的差值,如果该值小于最小绝对差,就用它更新最小绝对差。
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
TreeNode(int x,TreeNode * l,TreeNode * r) : val(x), left(l), right(r) {}
};
class Solution {
public:
vector<int> temp;
int getMinimumDifference(TreeNode* root) {
dfs(root);
int min = 1000000000;
for(int i = 1 ; i<temp.size() ; i++) {
int x = abs(temp[i-1] -temp[i]);
if(x <min) {
min = x;
}
}
return min;
}
void dfs(TreeNode* root)
{
if(!root) return;
dfs(root->left);
temp.push_back(root->val);
dfs(root->right);
}
};
|
538. 把二叉搜索树转换为累加树
给定一个二叉搜索树(Binary Search Tree),把它转换成为累加树(Greater
Tree),使得每个节点的值是原来的节点值加上所有大于它的节点值之和。

可以发现,右子树没有进行累加,而根结点累加了右子树,左子树累加了根和右子树。
所以应该从右子树开始递归遍历,将右子树的值加到根结点上,将所有根结点和右子树的值加到左子树上。
需要维护全局变量sum,来保存之前遍历的值,就可以从右想做将树的值累加。
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
TreeNode(int x,TreeNode * l,TreeNode * r) : val(x), left(l), right(r) {}
};
class Solution {
public:
int sum = 0;
TreeNode* convertBST(TreeNode* root) {
if(!root ) return NULL;
convertBST(root->right);
sum+=root->val;
root->val = sum;
convertBST(root->left);
return root;
}
};
|
543. 二叉树的直径
给定一棵二叉树,你需要计算它的直径长度。一棵二叉树的直径长度是任意两个结点路径长度中的最大值。这条路径可能穿过也可能不穿过根结点。
示例 :
给定二叉树
1
/ \
2 3
/ \
4 5
返回 3, 它的长度是路径 [4,2,1,3] 或者 [5,2,1,3]。
注意:两结点之间的路径长度是以它们之间边的数目表示。
深度优先搜索
由示例,我们知道一条路径的长度为该路径经过的节点数减一,所以求直径(即求路径长度的最大值)等效于求路径经过节点数的最大值减一。
而任意一条路径均可以被看作由某个节点为起点,从其左儿子和右儿子向下遍历的路径拼接得到。
假设我们知道对于该节点的左儿子向下遍历经过最多的节点数 L (即以左儿子为根的子树的深度) 和其右儿子向下遍历经过最多的节点数 R (即以右儿子为根的子树的深度)
则以该节点为起点的路径经过节点数的最大值为 L+R+1。
而以该节点为根的子树的深度为max(L,R)+1
所以得出递归算法:
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
TreeNode(int x,TreeNode * l,TreeNode * r) : val(x), left(l), right(r) {}
};
class Solution {
public:
int ans = 1;
int diameterOfBinaryTree(TreeNode* root) {
getDepth(root);
return ans -1;
}
int getDepth(TreeNode* root)
{
if(!root) return NULL;
int x = getDepth(root->left);
int y = getDepth(root->right);
ans = max(ans,x+y+1);
return max(x, y) +1;
}
};
|
563. 二叉树的坡度
给定一个二叉树,计算整个树的坡度。
一个树的节点的坡度定义即为,该节点左子树的结点之和和右子树结点之和的差的绝对值。空结点的的坡度是0。

我们需要在给定树的每个结点处找到其坡度,并将所有的坡度相加以获得最终结果。要找出任意结点的坡度,我们需要求出该结点的左子树上所有结点和以及其右子树上全部结点和的差值。
需要写一个函数,求出此节点以及其下面节点的和,以便求解差值。
借助于任何结点的左右子结点的这一和值,我们可以直接获得该结点所对应的坡度。
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
TreeNode(int x,TreeNode * l,TreeNode * r) : val(x), left(l), right(r) {}
};
class Solution {
public:
int ans = 0;
int findTilt(TreeNode* root) {
traverse(root);
return ans;
}
int traverse(TreeNode *root)
{
if(!root) return 0;
int left = traverse(root->left);
int right = traverse(root->right);
ans += abs(left-right);
return left+right+root->val;
}
};
|
572. 另一个树的子树
给定两个非空二叉树 s 和 t,检验 s 中是否包含和 t 具有相同结构和节点值的子树。s 的一个子树包括 s 的一个节点和这个节点的所有子孙。s 也可以看做它自身的一棵子树。


可以通过比较每个节点的值,来比较是否为子树
我们可以将给定树的每个节点 t作为根,将其作为子树,并将相应子树与给定子树 s 进行比较,以获得相等性。为了检查相等性,我们可以比较两个子树的所有节点。
为此,我们使用一个函数 isSubtree(s,t),它遍历给定的树 s 并将每个节点视为当前正在考虑的子树的根。它还检查当前考虑的两个子树是否相等。
为了检查两个子树的相等性,我们使用了 equals(x,y) 函数,它取 x 和 y作为要比较的两个子树的根作为输入,并根据两者是否相等返回 true 或 false。它比较两个子树的所有节点是否相等。
首先,它检查两个树的根是否相等,然后递归判断左子树和右子树。
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
TreeNode(int x,TreeNode * l,TreeNode * r) : val(x), left(l), right(r) {}
};
class Solution {
public:
bool isSubtree(TreeNode* s, TreeNode* t) {
if(!s) return false;
return isequal(s,t) || isSubtree(s->left,t) || isSubtree(s->right,t);
}
bool isequal(TreeNode* s, TreeNode* t){
if(!s && !t) return true;
if(!s || !t) return false;
return s->val == t->val && isequal(s->left,t->left) && isequal(s->right,t->right);
}
};
|
606. 根据二叉树创建字符串
你需要采用前序遍历的方式,将一个二叉树转换成一个由括号和整数组成的字符串。
空节点则用一对空括号 “()” 表示。而且你需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。


递归
我们可以使用递归的方法得到二叉树的前序遍历。在递归时,根据题目描述,我们需要加上额外的括号,会有以下 4 种情况:
(1)如果当前节点有两个孩子,那我们在递归时,需要在两个孩子的结果外都加上一层括号;
(2)如果当前节点没有孩子,那我们不需要在节点后面加括号;
(3)如果当前节点只有左孩子,那我们在递归时,只需要在左孩子的结果外加上一层括号,而不需要给右孩子加括号;
(4)如果当前节点只有右孩子,那我们在递归时,需要先加上一层空的括号 () 表示左孩子为空,再对右孩子进行递归,并在结果外加上一层括号。
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
TreeNode(int x,TreeNode * l,TreeNode * r) : val(x), left(l), right(r) {}
};
class Solution {
public:
string result = "";
string tree2str(TreeNode* t) {
if(t==NULL)
return "";
if(t->left==NULL && t->right==NULL)
return to_string(t->val)+"";
if(t->right==NULL)
return to_string(t->val)+"("+tree2str(t->left)+")";
return to_string(t->val)+"("+tree2str(t->left)+")("+tree2str(t->right)+")";
}
};
|
617. 合并二叉树
给定两个二叉树,想象当你将它们中的一个覆盖到另一个上时,两个二叉树的一些节点便会重叠。
你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠,那么将他们的值相加作为节点合并后的新值,否则不为 NULL 的节点将直接作为新二叉树的节点。

递归
我们可以对这两棵树同时进行前序遍历,并将对应的节点进行合并。
在遍历时,如果两棵树的当前节点均不为空,我们就将它们的值进行相加,并对它们的左孩子和右孩子进行递归合并;如果其中有一棵树为空,那么我们返回另一颗树作为结果;如果两棵树均为空,此时返回任意一棵树均可(因为都是空)。
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
TreeNode(int x,TreeNode * l,TreeNode * r) : val(x), left(l), right(r) {}
};
class Solution {
public:
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
if(!t1 ) return t2;
if(!t2 ) return t1;
t1->val +=t2->val;
t1->left = mergeTrees(t1->left, t2->left);
t1->right = mergeTrees(t1->right, t2->right);
return t1;
}
};
|
100. 相同的树
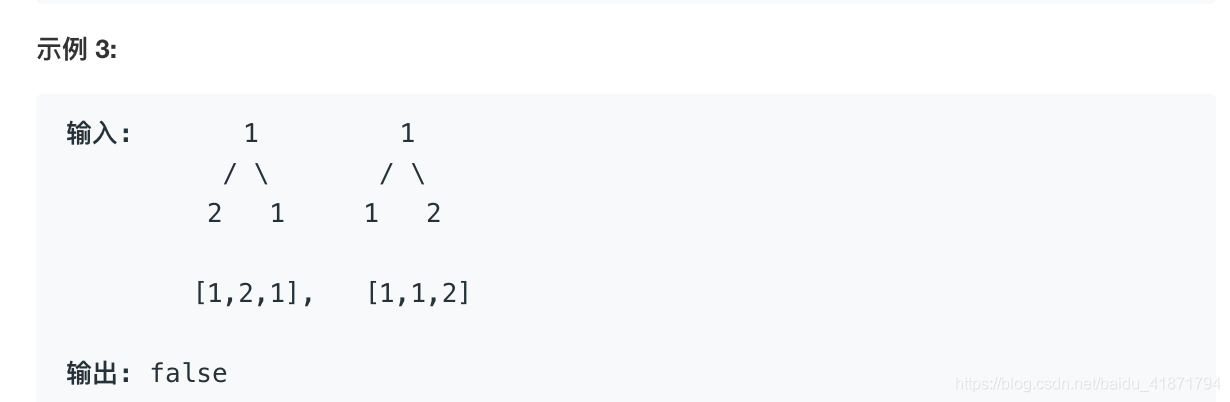
给定两个二叉树,编写一个函数来检验它们是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。

1.递归
首先判断 p 和 q 是不是 None,然后判断它们的值是否相等。
若以上判断通过,则递归对子结点做同样操作。
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
if(!p&&!q) return true;
if(p==NULL||q == NULL) return false;
if(q->val != p->val) return false;
return isSameTree(p->left, q->left) &&isSameTree(p->right, q->right);
}
};
|
2.使用队列进行迭代
从根开始,每次迭代将当前结点从双向队列中弹出。然后,进行判断:首先判断 p 和 q 是不是 None,然后判断它们的值是否相等。
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
if(!p&&!q) return true;
if (!check(p, q)) return false;
queue<TreeNode *> pqueue;
queue<TreeNode *> qqueue;
pqueue.push(p);
qqueue.push(q);
while (!pqueue.empty()) {
p = pqueue.front();
q = qqueue.front();
pqueue.pop();
qqueue.pop();
if (!check(p, q)) return false;
if( p)
{
if (!check(p->left, q->left)) return false;
}
if (p->left != NULL) {
pqueue.push(p->left);
qqueue.push(q->left);
}
if (!check(p->right, q->right)) return false;
if (p->right != NULL) {
pqueue.push(p->right);
qqueue.push(q->right);
}
}
return true;
}
bool check(TreeNode* p, TreeNode* q)
{
if(!p&&!q) return true;
if(p==NULL||q == NULL) return false;
if(q->val != p->val) return false;
return true;
}
};
|
101. 对称二叉树
给定一个二叉树,检查它是否是镜像对称的。
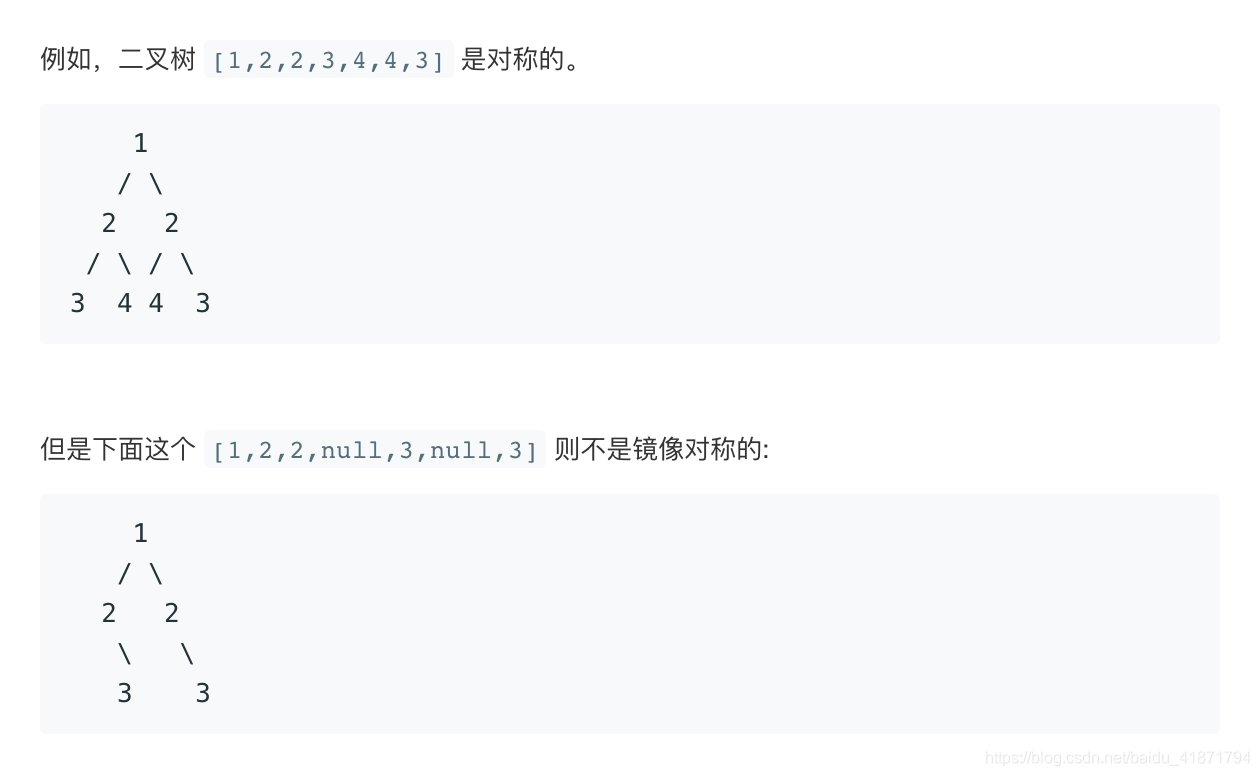
1.递归
进行递归判断:
(1)它们的两个根结点具有相同的值。
(2)每个树的右子树都与另一个树的左子树镜像对称。
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
bool isSymmetric(TreeNode* root) {
return isMirror(root, root);
}
bool isMirror(TreeNode* t1,TreeNode* t2)
{
if(t1 == NULL && t2 == NULL) return true;
if(t1 == NULL || t2 == NULL) return false;
return (t1->val == t2->val) &&isMirror(t1->left,t2->right) &&isMirror(t1->right,t2->left);
}
};
|
2.使用队列进行迭代
队列中每两个连续的结点应该是相等的,而且它们的子树互为镜像。最初,队列中包含的是 root 以及 root。
每次提取两个结点并比较它们的值。然后,将两个结点的左右子结点按相反的顺序插入队列中。当队列为空时,或者我们检测到树不对称(即从队列中取出两个不相等的连续结点)时,该算法结束。
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
bool isSymmetric(TreeNode* root) {
queue<TreeNode *> q;
q.push(root);
q.push(root);
TreeNode* t1;
TreeNode* t2;
while (!q.empty()) {
t1 = q.front();
q.pop();
t2 = q.front();
q.pop();
if(t1 ==NULL&&t2 ==NULL) continue;
if(t1 == NULL || t2 == NULL ) return false;
if(t1->val != t2->val) return false;
q.push(t1->left);
q.push(t2->right);
q.push(t1->right);
q.push(t2->left);
}
return true;
}
};
|
104. 二叉树的最大深度
给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。

1.递归
递归求左子树深度和右子树深度,当前的深度为左右子树深度+1的最大值
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
int depth =0;
int maxDepth(TreeNode* root) {
if(root==NULL) return 0;
int l=maxDepth(root->left)+1;
int r=maxDepth(root->right)+1;
return l>r?l:r;
}
};
|
2.使用队列进行BFS
每次遍历到下一层,则深度+1,最终返回
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
int depth =0;
int maxDepth(TreeNode* root) {
if (root == NULL) {
return 0;
}
queue<TreeNode * > q;
q.push(root);
while (!q.empty()) {
depth ++;
int levelSize = q.size();
for(int i = 0 ; i<levelSize ; i++)
{
TreeNode * t1 = q.front();
q.pop();
if(t1->left )
{
q.push(t1->left);
}
if(t1->right )
{
q.push(t1->right);
}
}
}
return depth;
}
};
|
3.借助堆栈进行DFS
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
int depth =0;
int maxDepth(TreeNode* root) {
if (root == NULL) {
return 0;
}
stack<pair<TreeNode*,int>> s;
TreeNode * t1 =root;
int x = 0;
while (!s.empty() || t1 != NULL) {
while (t1!=NULL)
{
s.push(pair<TreeNode*,int>(t1,++x));
t1 = t1->left;
}
t1 = s.top().first;
x = s.top().second;
s.pop();
if(depth<x) depth=x;
t1=t1->right;
}
return depth;
}
};
|
107. 二叉树的层次遍历 II
给定一个二叉树,返回其节点值自底向上的层次遍历。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)

二叉树层序遍历即可,每遍历一层,就讲结果push到vector的首部(要注意顺序,树的最后一层为数组的第一个元素)
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
TreeNode(int x, TreeNode *a, TreeNode *b) : val(x), left(a), right(b) {}
};
class Solution {
public:
vector<vector<int>> result;
vector<vector<int>> levelOrderBottom(TreeNode* root) {
if(root ==NULL)
{
return result;
}
queue<TreeNode *> q;
q.push(root);
while (!q.empty()) {
vector<int> a ;
int x = q.size();
for(int i = 0 ; i <x ; i++)
{
TreeNode * t1 = q.front();
q.pop();
a.push_back(t1->val);
if(t1->left)
{
q.push(t1->left);
}
if(t1->right)
{
q.push(t1->right);
}
}
result.insert(result.begin(), a);
}
return result;
}
};
|
108. 将有序数组转换为二叉搜索树
将一个按照升序排列的有序数组,转换为一棵高度平衡二叉搜索树。
本题中,一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。

中序遍历不能唯一确定一棵二叉搜索树。
先序和后序遍历不能唯一确定一棵二叉搜索树。
中序+后序、中序+先序可以唯一确定一棵二叉树。
而题目说:
树的高度应该是平衡的、例如:每个节点的两棵子树高度差不超过 1。
对于奇数个数的数组,高度平衡意味着每次必须选择中间数字作为根节点,创建的二叉树是唯一的。
对于偶数个数的数组,要么选择中间位置左边的元素作为根节点,要么选择中间位置右边的元素作为根节点,不同的选择方案会创建不同的平衡二叉搜索树。
作者:LeetCode
链接:https://leetcode-cn.com/problems/convert-sorted-array-to-binary-search-tree/solution/jiang-you-xu-shu-zu-zhuan-huan-wei-er-cha-sou-s-15/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
中序遍历,始终选择中间位置右边元素作为根节点:
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
TreeNode* sortedArrayToBST(vector<int>& nums) {
return helper(0, nums.size() - 1,nums);
}
TreeNode* helper(int left,int right,vector<int>& nums)
{
if (left > right) return NULL;
int p = (left + right) / 2;
if ((left + right) % 2 == 1) ++p;
TreeNode * root = new TreeNode(nums[p]);
root->left = helper(left, p - 1,nums);
root->right = helper(p + 1, right,nums);
return root;
}
};
|
110. 平衡二叉树
给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:
一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。
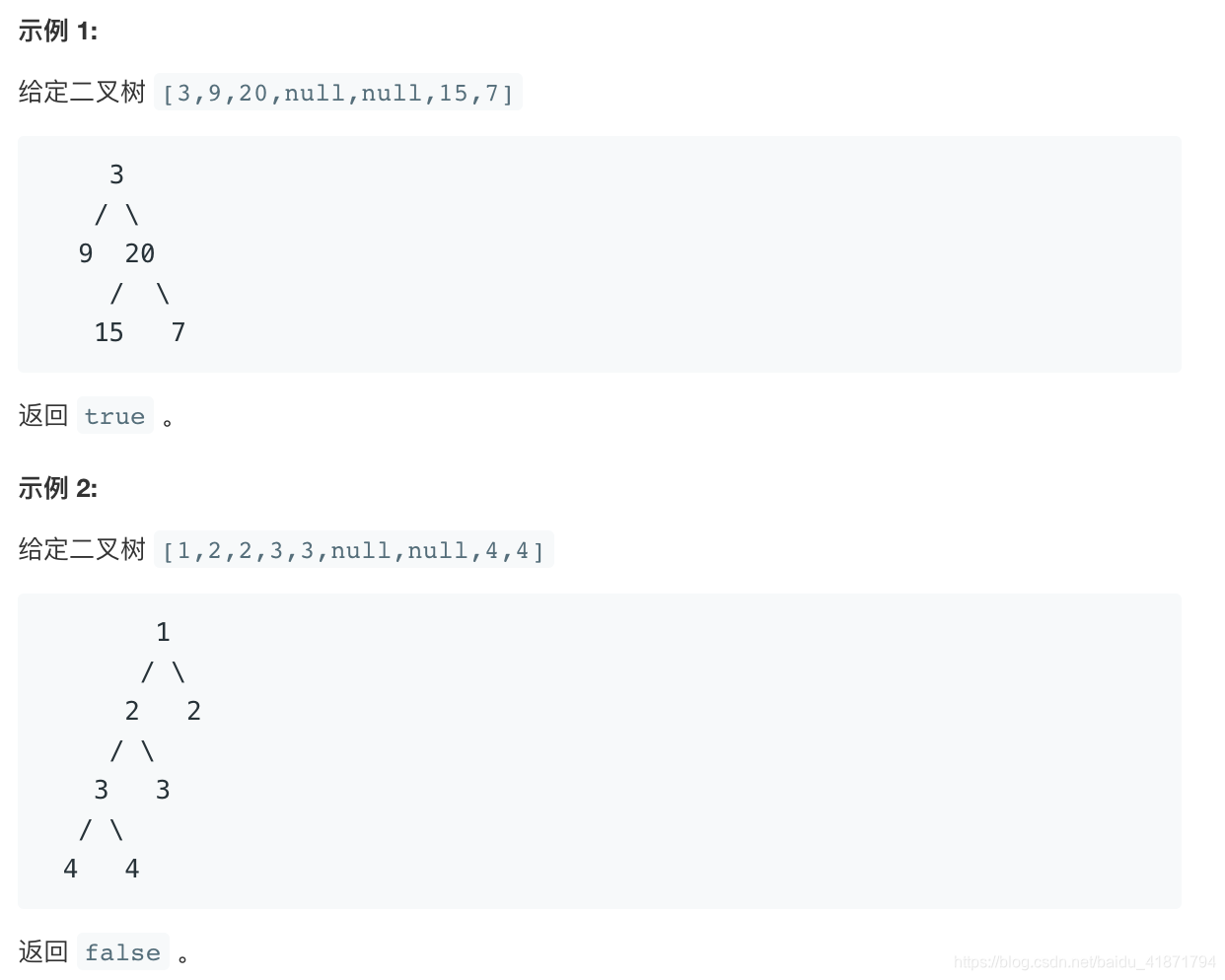
自顶向下的递归:
首先计算每一个节点的左子树高度和右子树高度,较大的值+1为以此节点为根的树的高度
然后需要判断,此节点的左右子树是否平衡,如果平衡则递归到此节点的左右子树进行判断。
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
int height(TreeNode* root)
{
if(!root)return -1;
return 1+max(height(root->left),height(root->right));
}
bool isBalanced(TreeNode* root) {
if (root == NULL) {
return true;
}
return abs(height(root->left) - height(root->right)) < 2 &&
isBalanced(root->left) &&
isBalanced(root->right);
}
};
|
111. 二叉树的最小深度
给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
说明: 叶子节点是指没有子节点的节点。

1.递归DFS:
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
TreeNode(int x,TreeNode * l,TreeNode * r) : val(x), left(l), right(r) {}
};
class Solution {
public:
int minDepth(TreeNode* root) {
return dfs(root);;
}
int dfs(TreeNode* root)
{
if(!root) return 0;
if(!root->left && ! root->right) return 1;
int m1 = dfs(root->left);
int m2 = dfs(root->right);
if(!root->left || !root->right ) return m1 + m2 + 1;
return min(m1,m2) + 1;
}
};
|
2.非递归DFS
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
TreeNode(int x,TreeNode * l,TreeNode * r) : val(x), left(l), right(r) {}
};
class Solution {
public:
int minDepth(TreeNode* root) {
return dfs3(root);;
}
int dfs(TreeNode* root)
{
stack<pair<TreeNode *, int>> s;
if(!root) return 0;
s.push(pair<TreeNode *, int>(root,1));
int min_depth = 100000000;
while (!s.empty()) {
pair<TreeNode *, int> t1 = s.top();
s.pop();
if(t1.first->left == NULL&& t1.first->right== NULL)
{
min_depth = min(min_depth,t1.second);
}
if (t1.first->left != NULL) {
s.push(pair<TreeNode *, int>(t1.first->left,t1.second+1));
}
if (t1.first->right != NULL) {
s.push(pair<TreeNode *, int>(t1.first->right,t1.second+1));
}
}
return min_depth;
}
};
|
3.BFS
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
TreeNode(int x,TreeNode * l,TreeNode * r) : val(x), left(l), right(r) {}
};
class Solution {
public:
int minDepth(TreeNode* root) {
return dfs3(root);;
}
int dfs(TreeNode* root)
{
queue<pair<TreeNode *, int>> q;
if(!root) return 0;
q.push(pair<TreeNode *, int>(root,1));
int min_depth = 0;
while (!q.empty()) {
pair<TreeNode *, int> t1 = q.front();
q.pop();
min_depth = t1.second;
if(t1.first->left == NULL&& t1.first->right== NULL)
{
break;
}
if (t1.first->left != NULL) {
q.push(pair<TreeNode *, int>(t1.first->left,min_depth+1));
}
if (t1.first->right != NULL) {
q.push(pair<TreeNode *, int>(t1.first->right,min_depth+1));
}
}
return min_depth;
}
};
|
112. 路径总和
给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。
说明: 叶子节点是指没有子节点的节点。
1.递归DFS
遍历整棵树:如果当前节点不是叶子,对它的所有孩子节点,递归调用 dfs 函数,其中 sum 值减去当前节点的权值;如果当前节点是叶子,检查 sum 值是否与叶节点的值相同,也就是是否找到了给定的目标和。
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
bool hasPathSum(TreeNode* root, int sum) {
return dfs(root,sum);
}
bool dfs(TreeNode* root, int sum)
{
if(!root) return false;
if(root->left == NULL &&root->right == NULL)
{
if(root->val == sum)
{
return true;
}
}
return (dfs(root->left, sum - root->val)||dfs(root->right, sum -root->val));
}
};
|
2.递归DFS2
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
bool hasPathSum(TreeNode* root, int sum) {
bool flag = false;
vector<int> path;
dfs(root,sum, path, flag);
return flag;
}
void dfs(TreeNode* root, int &sum ,vector<int> & path,bool &flag)
{
if(!root) return;
path.push_back(root->val);
int ans = 0;
if(!root->left &&!root->right)
{
for(int i = path.size()-1 ; i>=0 ; i--)
{
ans +=path[i];
}
if(ans == sum)
{
flag = true;
}
}
dfs(root->left,sum,path,flag);
dfs(root->right,sum,path,flag);
path.pop_back();
}
};
|
637. 二叉树的层平均值
给定一个非空二叉树, 返回一个由每层节点平均值组成的数组.
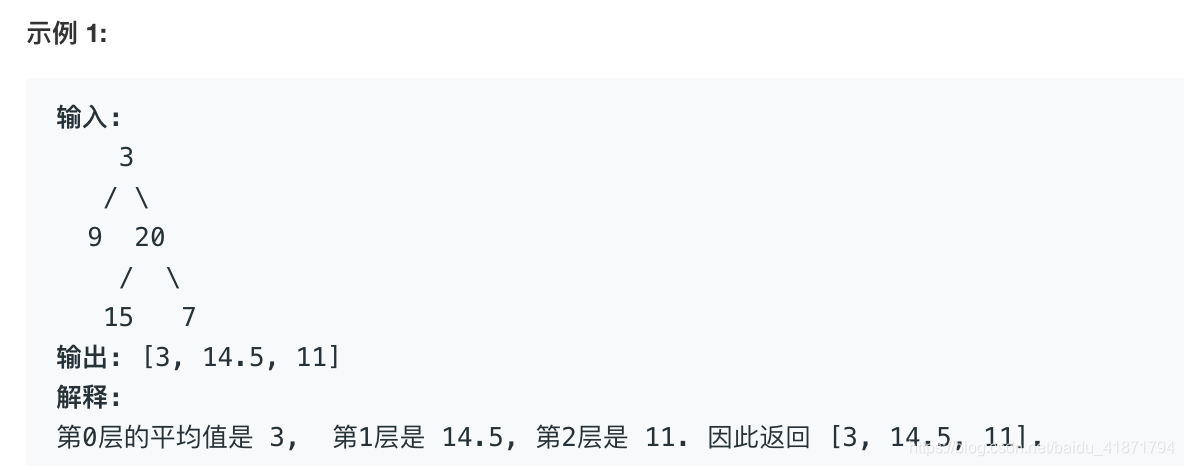
逐层遍历即可
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
TreeNode(int x,TreeNode * l,TreeNode * r) : val(x), left(l), right(r) {}
};
class Solution {
public:
vector<double> result;
vector<double> averageOfLevels(TreeNode* root) {
queue<TreeNode *> q;
q.push(root);
while (!q.empty()) {
int size = q.size();
double sum = 0;
for(int i = 0 ; i<size ; i++)
{
TreeNode * t1 = q.front();
q.pop();
sum+=t1->val;
if(t1->left ) q.push(t1->left);
if(t1->right) q.push(t1->right);
}
result.push_back(sum/size);
}
return result;
}
};
|
671. 二叉树中第二小的节点
给定一个非空特殊的二叉树,每个节点都是正数,并且每个节点的子节点数量只能为 2 或0。如果一个节点有两个子节点的话,那么这个节点的值不大于它的子节点的值。
给出这样的一个二叉树,你需要输出所有节点中的第二小的值。如果第二小的值不存在的话,输出 -1 。

第一个最小值必须是 root->val
然后遍历左右子树,寻找第二小的值
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
TreeNode(int x,TreeNode * l,TreeNode * r) : val(x), left(l), right(r) {}
};
class Solution {
public:
int secondMin = -1;
int findSecondMinimumValue(TreeNode* root) {
if(root == NULL || (root->left == NULL&&root->right == NULL))
{
return -1;
}
queue<TreeNode *> q ;
q.push(root->left);
q.push(root->right);
while (!q.empty()) {
TreeNode * t = q.front();
q.pop();
if(t == NULL||t->val == secondMin)
{
continue;
}
else if((t->val>root->val&& secondMin == -1) ||(t->val<secondMin && t->val>root->val))
{
secondMin = t->val;
}
else
{
if(t->left!=NULL){
q.push(t->left);
}
if(t->right!=NULL){
q.push(t->right);
}
}
}
return secondMin;
}
};
|
226. 翻转二叉树
翻转一棵二叉树。

1.递归
使用递归翻转左右子树,然后在反转自身
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
TreeNode(int x,TreeNode * l,TreeNode * r) : val(x), left(l), right(r) {}
};
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if(root == NULL) return NULL;
TreeNode *right = invertTree(root->right);
TreeNode *left = invertTree(root->left);
root->left = right;
root->right = left;
return root;
}
};
|
2.非递归
我们需要交换树中所有节点的左孩子和右孩子。因此可以创一个队列来存储所有左孩子和右孩子还没有被交换过的节点。开始的时候,只有根节点在这个队列里面。只要这个队列不空,就一直从队列中出队节点,然后互换这个节点的左右孩子节点,接着再把孩子节点入队到队列,对于其中的空节点不需要加入队列。最终队列一定会空,这时候所有节点的孩子节点都被互换过了,直接返回最初的根节点就可以了。
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
TreeNode(int x,TreeNode * l,TreeNode * r) : val(x), left(l), right(r) {}
};
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if(root == NULL) return NULL;
queue<TreeNode *> q ;
q.push(root);
while (!q.empty()) {
TreeNode * t = q.front();
q.pop();
TreeNode * temp = t->left;
t->left = t->right;
t->right = temp;
if (t->left != NULL) q.push(t->left);
if (t->right != NULL) q.push(t->right);
}
return root;
}
};
|
235. 二叉搜索树的最近公共祖先
给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为:“对于有根树 T 的两个结点 p、q,最近公共祖先表示为一个结点 x,满足 x 是 p、q 的祖先且 x
的深度尽可能大(一个节点也可以是它自己的祖先)。”
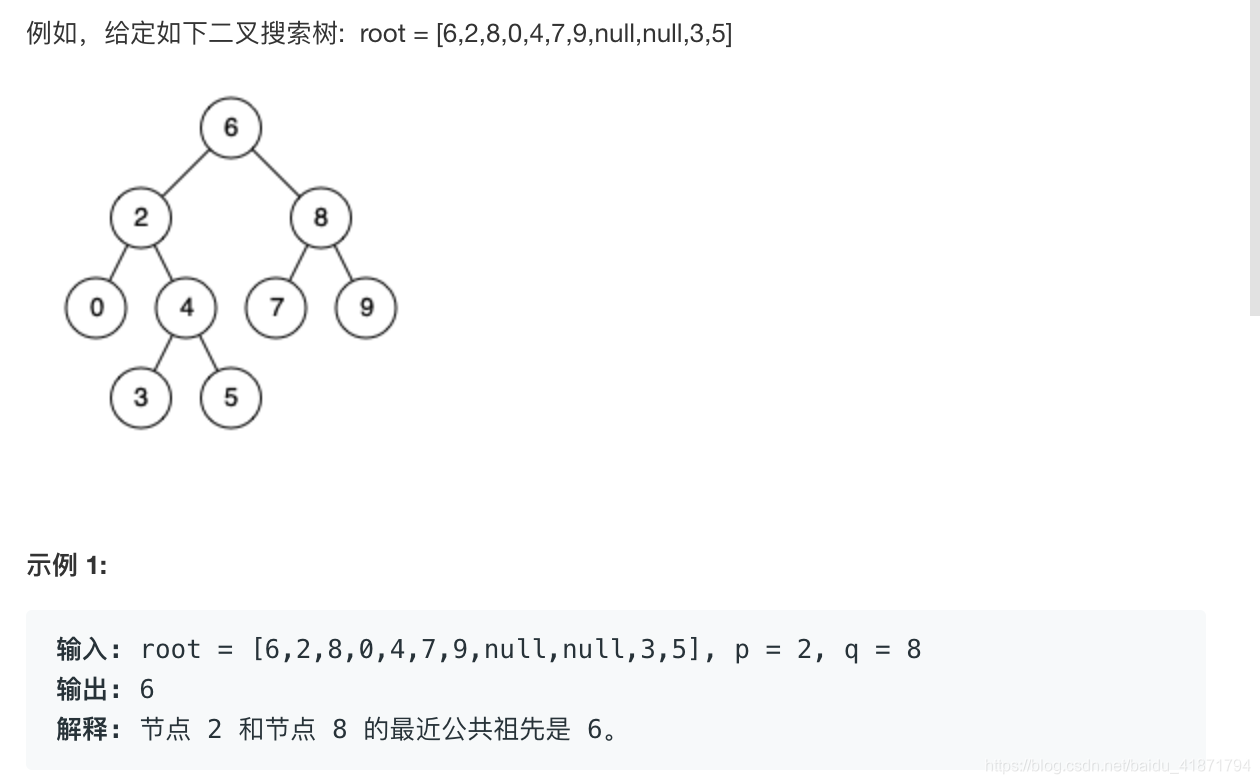

二叉搜索树(BST)的性质:
(1)节点 N 左子树上的所有节点的值都小于等于节点 N 的值
(2)节点 N 右子树上的所有节点的值都大于等于节点 N 的值
(3)左子树和右子树也都是 BST
1.递归:
(1)根节点开始遍历树
(2)如果节点 p 和节点 q 都在右子树上,那么以右孩子为根节点继续 (1) 的操作
(3)如果节点 pp 和节点 qq 都在左子树上,那么以左孩子为根节点继续 (1) 的操作
(4)如果条件 2 和条件 3 都不成立,这就意味着我们已经找到节 p 和节点 q 的最小公共祖先了
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
TreeNode(int x,TreeNode * l,TreeNode * r) : val(x), left(l), right(r) {}
};
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
int val = root->val;
int pval = p->val;
int qval = q->val;
if(pval>val &&qval>val)
{
return lowestCommonAncestor(root->right,p, q);
}
else if(qval<val &&pval<val)
{
return lowestCommonAncestor(root->left,p, q);
}
else
{
return root;
}
}
};
|
2.迭代
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
TreeNode(int x,TreeNode * l,TreeNode * r) : val(x), left(l), right(r) {}
};
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
int pval = p->val;
int qval = q->val;
TreeNode * node = root;
while (node!=NULL) {
int val = node->val;
if(pval>val &&qval>val)
{
node = node->right;
}
else if(qval<val &&pval<val)
{
node = node->left;
}
else
{
return node;
}
}
return NULL;
}
};
|
257. 二叉树的所有路径
给定一个二叉树,返回所有从根节点到叶子节点的路径。
说明: 叶子节点是指没有子节点的节点。

递归进行DFS
如果是叶子节点,则将路径push到结果数组result中,如果不是叶子节点,则继续遍历,最终将结果格式化输出(路径之间添加->)
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
vector<vector<int>> result;
vector<string> binaryTreePaths(TreeNode* root) {
vector<string> s;
vector<int> path;
dfs(root, path);
for(int i = 0 ; i <result.size() ; i++)
{
vector<int> temp = result[i];
string str = "";
for(int j = 0 ; j < temp.size()-1 ; j++)
{
str += to_string(temp[j])+"->";
}
str +=to_string(temp[temp.size()-1]);
s.push_back(str);
}
return s;
}
void dfs(TreeNode* root , vector<int> &path)
{
if(!root) return;
path.push_back(root->val);
if(!root->left &&!root->right)
{
result.push_back(path);
}
dfs(root->left,path);
dfs(root->right, path);
path.pop_back();
}
};
|
404. 左叶子之和
计算给定二叉树的所有左叶子之和。

struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
TreeNode(int x,TreeNode * l,TreeNode * r) : val(x), left(l), right(r) {}
};
class Solution {
public:
int ans = 0;
int sumOfLeftLeaves(TreeNode* root) {
dfs(root, false);
return ans;
}
void dfs(TreeNode* root,bool isLeft)
{
if(!root) return;
if(root->left == NULL &&root->right == NULL &&isLeft)
{
ans +=root->val;
}
dfs(root->left, true);
dfs(root->right, false);
}
};
|
437. 路径总和 III
给定一个二叉树,它的每个结点都存放着一个整数值。
找出路径和等于给定数值的路径总数。
路径不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。
二叉树不超过1000个节点,且节点数值范围是 [-1000000,1000000] 的整数。

把每个遍历到的节点当作终点(路径必须包含终点),记录根到终点的路径,从路径往前搜索,如果和等于sum则为一条路径
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
int pathSum(TreeNode* root, int sum) {
vector<int> path;
int count = 0;
dfs(root,path,sum,count);
return count;
}
void dfs(TreeNode *root ,vector<int> & path,int & sum,int & count)
{
if(!root) return;
path.push_back(root->val);
int cur = 0;
for(int i = path.size()-1 ; i>= 0 ; i--)
{
cur +=path[i];
if(cur == sum) count++;
}
dfs(root->left,path,sum,count);
dfs(root->right,path,sum,count);
path.pop_back();
}
};
|
501. 二叉搜索树中的众数
给定一个有相同值的二叉搜索树(BST),找出 BST 中的所有众数(出现频率最高的元素)。
假定 BST 有如下定义:
(1)结点左子树中所含结点的值小于等于当前结点的值
(2)结点右子树中所含结点的值大于等于当前结点的值
(3)左子树和右子树都是二叉搜索树

1.先中序遍历得到BST中的所有元素,然后在寻找众数
(中序遍历BST的结果是有序的)
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
TreeNode(int x,TreeNode * l,TreeNode * r) : val(x), left(l), right(r) {}
};
class Solution {
public:
vector<int> result;
vector<int> temp;
int max = 0;
int cur = 0;
vector<int> findMode(TreeNode* root) {
inorder(root);
if(temp.size() == 1)
{
result.push_back(temp[0]);
}
for(int i = 1 ; i<temp.size() ; i++)
{
if(temp[i] == temp[i-1])
{
cur++;
}
else
{
cur = 0;
}
if(cur == max)
{
if(i==1 && cur ==0)
{
result.push_back(temp[0]);
}
result.push_back(temp[i]);
}
else if(cur>max)
{
result.clear();
max = cur;
result.push_back(temp[i]);
}
}
return result;
}
void inorder(TreeNode* root)
{
if(!root) return;
inorder(root->left);
temp.push_back(root->val);
inorder(root->right);
}
};
|

































