leetcode刷题——树（中等）

leetcode刷题记录，有关树的中等难度算法题

94. 二叉树的中序遍历

给定一个二叉树，返回它的中序遍历。

1.非递归中序遍历

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
    vector<int> result;
    vector<int> inorderTraversal(TreeNode* root) {
       
        
        stack<TreeNode*> stack;
        TreeNode * cur = root;
        while (cur || !stack.empty()) {
            while (cur ) {
                stack.push(cur);
                cur = cur->left;
            }
            cur = stack.top();
            stack.pop();
            result.push_back(cur->val);
            cur = cur->right;
            
        }
        return result;
    }
    
};

2.递归中序遍历

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
    vector<int> result;
    vector<int> inorderTraversal(TreeNode* root) {
      
        return result;
    }
    void postorder(TreeNode *root)
    {
        if(!root) return;
        postorder(root->left);
        result.push_back(root->val);
        postorder(root->right);
        
    }
};

95. 不同的二叉搜索树 II

给定一个整数 n，生成所有由 1 … n 为节点所组成的二叉搜索树。

我们从序列 1 …n 中取出数字 i，作为当前树的树根。于是，剩余 i - 1 个元素可用于左子树，n - i 个元素用于右子树。
如前文所述，这样会产生 G(i - 1) 种左子树和 G(n - i) 种右子树，其中 G 是卡特兰数
现在，我们对序列 1 … i - 1 重复上述过程，以构建所有的左子树；然后对 i + 1 … n 重复，以构建所有的右子树。
这样，我们就有了树根 i 和可能的左子树、右子树的列表。
最后一步，对两个列表循环，将左子树和右子树连接在根上。

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
    vector<TreeNode*> generateTrees(int n) {
        if(n == 0)
        {
            vector<TreeNode *> a;
            return a;
        }
        return generate_trees(1, n);
        
        
    }
    vector<TreeNode*> generate_trees(int start,int end) {
        vector<TreeNode*> all_trees;
        if (start > end) {
            all_trees.push_back(NULL);
            return all_trees;
        }
        for(int i = start ; i <=end ; i++)
            
        {
            vector<TreeNode*> left_trees = generate_trees(start,i-1);
            vector<TreeNode*> right_trees = generate_trees(i+1,end);
            for(int l = 0 ; l <left_trees.size() ; l++)
            {
                for(int r = 0 ; r < right_trees.size() ; r ++)
                {
                    TreeNode * current_tree = new TreeNode(i);
                    current_tree->left = left_trees[l];
                    current_tree->right = right_trees[r];
                    all_trees.push_back(current_tree);
                }
            }
        }
        return all_trees;
    }
};

96. 不同的二叉搜索树（动态规划！= =！难顶）

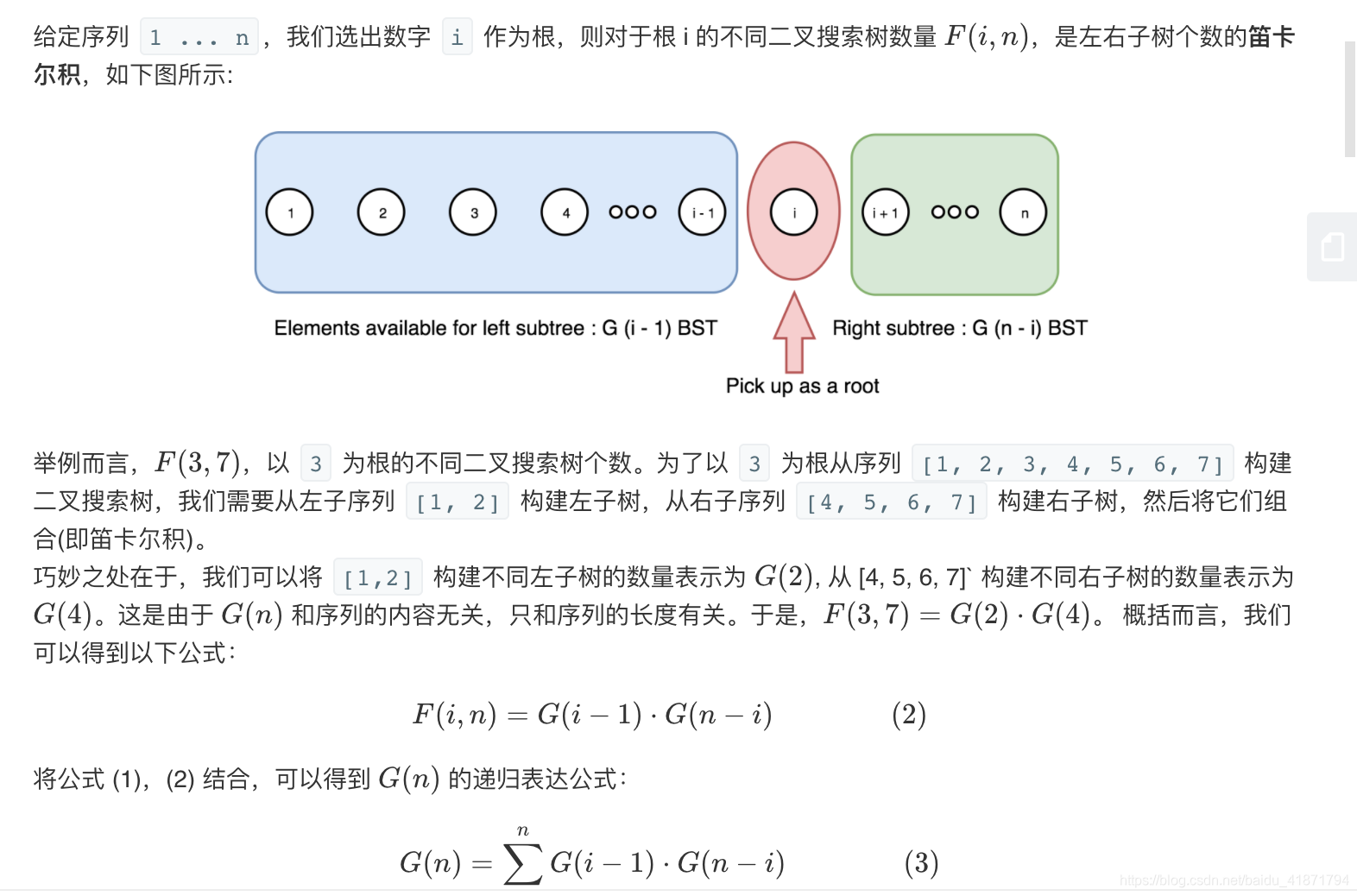
给定一个整数 n，求以 1 … n 为节点组成的二叉搜索树有多少种？

动态规划
给定一个有序序列 1 … n，为了根据序列构建一棵二叉搜索树。我们可以遍历每个数字 i，将该数字作为树根，1 … (i-1) 序列将成为左子树，(i+1) … n 序列将成为右子树。于是，我们可以递归地从子序列构建子树。

leetcode官方题解：

class Solution {
public:
    int numTrees(int n) {
        vector<int> dp(n + 1, 0);
        dp[0] = 1;
        dp[1] = 1;
        
        for(int i = 2; i <= n; i++)
            for(int j = 1; j <= i; j++){
                dp[i] += dp[j - 1] * dp[i - j];
            }
        return dp[n];
    }
};

98. 验证二叉搜索树

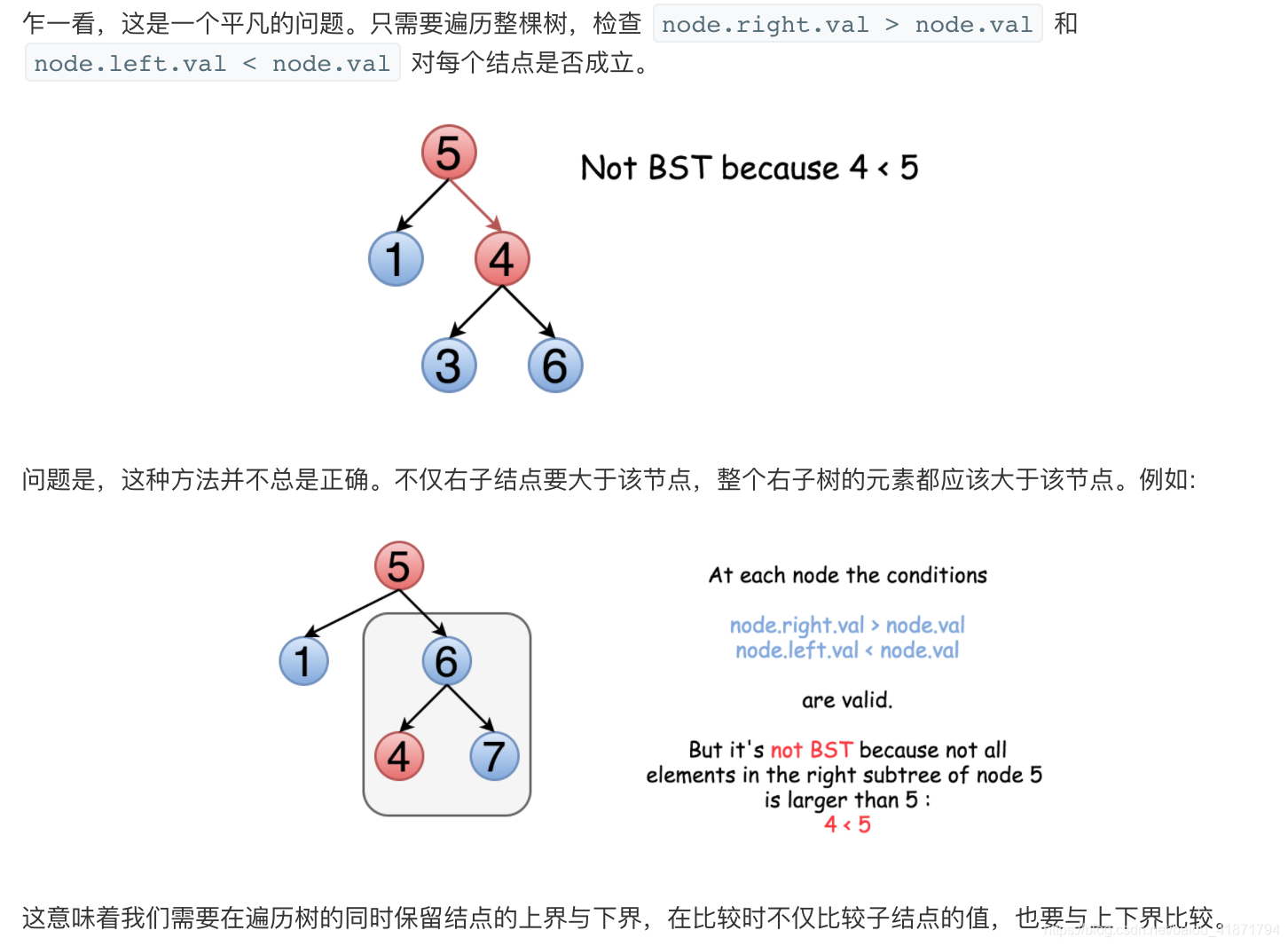
给定一个二叉树，判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征：
（1）节点的左子树只包含小于当前节点的数。
（2）节点的右子树只包含大于当前节点的数。
（3）所有左子树和右子树自身必须也是二叉搜索树。

在这里插入图片描述
注意（官方题解提示）：

1.递归判断
首先将结点的值与上界和下界（如果有）比较。然后，对左子树和右子树递归进行该过程。

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:

    bool isValidBST(TreeNode* root) {
        return judge(root, LONG_MIN,LONG_MAX);
    }
    bool judge(TreeNode * root, long low, long  up)
    {
        if(root == nullptr) return true;
        long val = root->val;
        if(val<=low || val>=up) return false;
        return judge(root->left,low,val) &&judge(root->right,val,up);
    }
    
};

2.中序遍历
左子树 -> 结点 -> 右子树
对于二叉搜索树而言，每个元素都应该比下一个元素小

class Solution {
public:

    bool isValidBST(TreeNode* root) {
        stack<TreeNode *> s;
        while (root !=NULL || !s.empty()) {
            while (root != NULL) {
                s.push(root);
                root = root->left;
            }
            root = s.top();
            s.pop();
            if (root->val <= min) return false;
            min = root->val;
            root = root->right;
        }
        
                return true;
    
    }
 
};

113. 路径总和 II

给定一个二叉树和一个目标和，找到所有从根节点到叶子节点路径总和等于给定目标和的路径。
说明: 叶子节点是指没有子节点的节点。

按照递归的方法依次遍历左右子树各个结点。
如果到叶节点则判断是否路径要求。
利用回溯思想将每次目标路径的数组元素回退到上一个结点，之后遍历另一条边的结点寻找更多的可能性

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
    vector<vector<int>> result;
    vector<vector<int>> pathSum(TreeNode* root, int sum) {
        vector<int> path;
        dfs(root,sum,path);
        return result;
    }
    void dfs(TreeNode* root, int sum,vector<int> & path)
    {
        if(!root) return;
        path.push_back(root->val);
        //如果左右都为空 表示此时递归到了叶子结点 此时判断和是否等于sum
        if(!root->left && !root->right)
        {
            int s = 0;
            for(int i = path.size()-1 ; i>= 0 ; i--)
            {
                s+= path[i];
                
            }
            if(s == sum)
            {
                result.push_back(path);
            }
        }
        //递归判断左右节点
        dfs(root->left, sum, path);
        dfs(root->right, sum, path);
        path.pop_back();
        
        
    }
};

129. 求根到叶子节点数字之和

给定一个二叉树，它的每个结点都存放一个 0-9 的数字，每条从根到叶子节点的路径都代表一个数字。

例如，从根到叶子节点路径 1->2->3 代表数字 123。

计算从根到叶子节点生成的所有数字之和。

说明: 叶子节点是指没有子节点的节点。

对树进行DFS，没到一个不是叶节点的新节点就将其组成数字，到叶节点则加到总和sum中

struct TreeNode {
     int val;
     TreeNode *left;
     TreeNode *right;
     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 };
class Solution {
public:
    int sum = 0;
    
    int sumNumbers(TreeNode* root) {
        dfs(root, 0);
        return sum;
    }
    void dfs(TreeNode* root,int x)
    {
        if(!root)return;
        x = x*10+root->val;
        if(!root->left && !root->right)
        {
            sum +=x;
            
        }
        dfs(root->left, x);
        dfs(root->right, x);
    }
};

144. 二叉树的前序遍历

1.递归

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

class Solution {
public:
    vector<int> result;
    vector<int> preorderTraversal(TreeNode* root) {
                preorderorder(root);
    }
    void preorderorder(TreeNode *root)
    {
        if(!root) return;

        result.push_back(root->val);
        preorderorder(root->left);

        preorderorder(root->right);

    }
};

2.非递归
创建一个Stack用来存放节点
首先我们想要打印根节点的数据，此时Stack里面的内容为空，所以我们优先将头结点加入Stack，然后打印。
之后我们应该先打印左子树，然后右子树。所以先加入Stack的就是右子树，然后左子树。

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

class Solution {
public:
    vector<int> result;
    vector<int> preorderTraversal(TreeNode* root) {
        
        if(!root)
        {
            return result;
        }
        stack<TreeNode*> stack;
        
        stack.push(root);
        while ( !stack.empty()) {
            TreeNode * node = stack.top();
            stack.pop();
            result.push_back(node->val);
            if (node->right ) {
                stack.push(node->right);
            }
            if (node->left ) {
                stack.push(node->left);
            }
            
            
            
        }
        return result;
    }
    
};

684. 冗余连接

在本问题中, 树指的是一个连通且无环的无向图。

输入一个图，该图由一个有着N个节点 (节点值不重复1, 2, …, N)
的树及一条附加的边构成。附加的边的两个顶点包含在1到N中间，这条附加的边不属于树中已存在的边。

结果图是一个以边组成的二维数组。每一个边的元素是一对[u, v] ，满足 u < v，表示连接顶点u 和v的无向图的边。

返回一条可以删去的边，使得结果图是一个有着N个节点的树。如果有多个答案，则返回二维数组中最后出现的边。答案边 [u, v] 应满足相同的格式u < v。

1.并查集
（1）初始化
刚开始每个元素都是一个独立的集合，需要令所有的father[i]=i；

（2）查找
find(node x)，找到元素 x 所在的集合的代表，该操作也可以用于判断两个元素是否位于同一个集合。
实现的方式可以是递归或者迭代，思路都是反复寻找父亲节点，直到根节点
（3）合并
union(node x, node y)，把元素 x 和元素 y 所在的集合合并，要求 x和 y 所在的集合不相交，如果相交则不合并。
合并的过程是将一个集合的根节点的父亲指向另一个集合的根结点

class Solution {
public:
    int parent[1001];
    int findFather(int x)
    {
    		//不断寻找父亲，直到根结点
        while (x !=findFather(x)) {
            parent[x] = parent[parent[x]];
            x = parent[x];
        }
        return x;
    }
    bool union_root(int x, int y) {
        int root_x = findFather(x);
        int root_y = findFather(y);
        //如果是同一集合 则不合并
        if (root_x == root_y) {
            return false;
        }
         //否则合并
        parent[root_x] = root_y;
        return true;
    }
    
    
    vector<int> findRedundantConnection(vector<vector<int>>& edges) {
    //初始化
        for(int i = 0 ; i< 1001; i ++)
        {
            parent[i] = i;
            
        }
        for (auto edge : edges) {
            if (!union_root(edge[0], edge[1])) {
                return edge;
            }
        }
        return {};
        
        
    }
    
};

2.DFS
对于每个边 (u, v)，用深度优先搜索遍历图，以查看是否可以将 u 连接到 v。如果可以，则它是重复边

988. 从叶结点开始的最小字符串

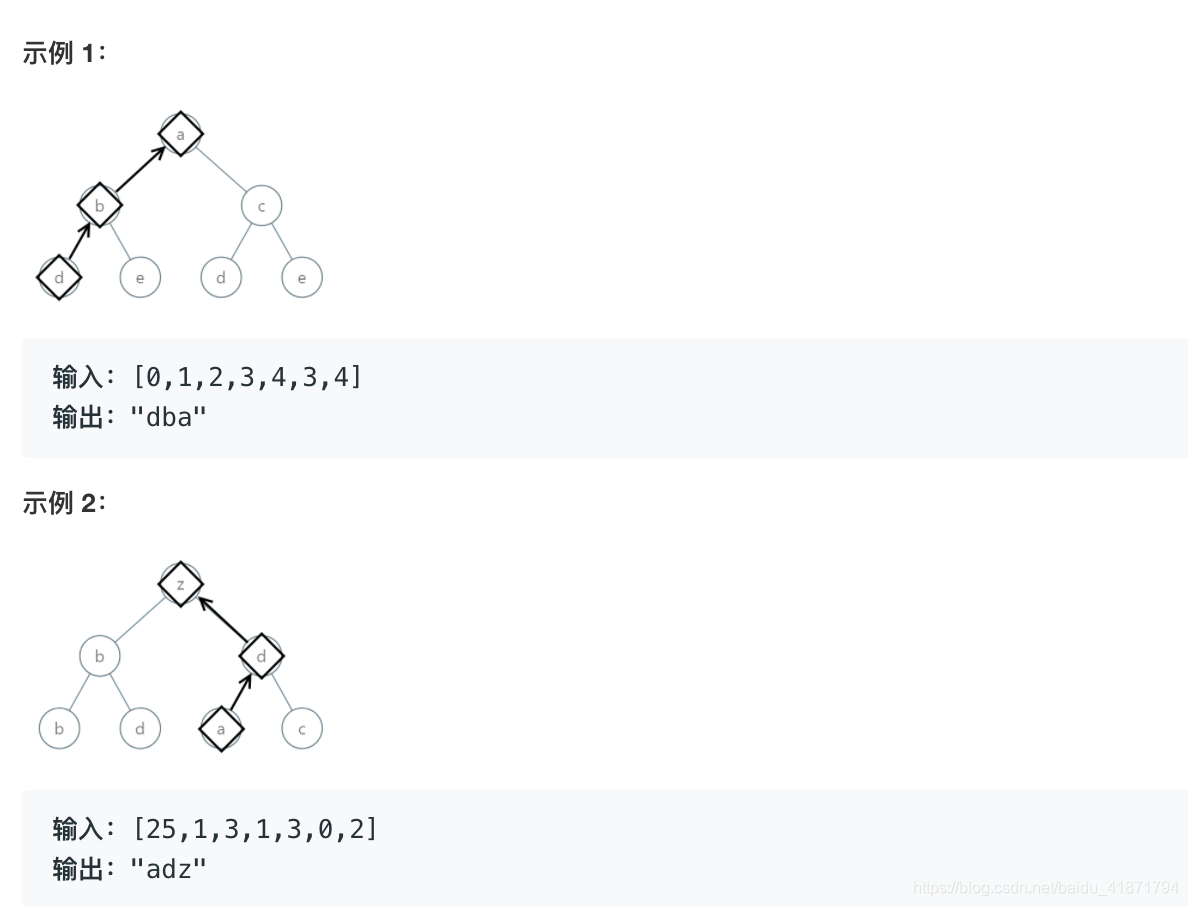
给定一颗根结点为 root 的二叉树，树中的每一个结点都有一个从 0 到 25 的值，分别代表字母 ‘a’ 到 ‘z’：值 0 代表
‘a’，值 1 代表 ‘b’，依此类推。

找出按字典序最小的字符串，该字符串从这棵树的一个叶结点开始，到根结点结束。

（小贴士：字符串中任何较短的前缀在字典序上都是较小的：例如，在字典序上 “ab” 比 “aba” 要小。叶结点是指没有子结点的结点。）

暴力破解：
创建出所有可能的字符串，然后逐一比较，输出字典序最小的那个。
在我们深度优先搜索的过程中，不断调整根到这个节点的路径上的字符串内容。
当我们到达一个叶子节点的时候，我们翻转路径的字符串内容来创建一个候选答案。如果候选答案比当前答案要优秀，那么我们更新答案。

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};
class Solution {
public:
    string ans = "z";
    string smallestFromLeaf(TreeNode* root) {
        dfs(root, "");
        return ans;
    }
    void reverse(string & s)
    {
        int len = s.size()-1;
        int mid = len/2;
        int i = 0;
        while(i<=mid){
            char temp = s[i];
            s[i] = s[len-i];
            s[len-i] = temp;
            i++;    }
    }
    void dfs(TreeNode* root,string s)
    {
        if(!root) return;
        s +=char('a'+root->val);
        //如果到了叶节点
        if(!root->left && !root->right)
        {
            reverse(s);
            if(s<ans)
            {
                ans = s;  }
        }
        dfs(root->left, s);
        dfs(root->right, s);
    }
};