PTA甲级刷题记录——图算法专题

PTA甲级刷题记录——图算法题解，方便自己复盘

A1003 Emergency (25分)(最短路径)

Sample Input:
5 6 0 2
1 2 1 5 3
0 1 1
0 2 2
0 3 1
1 2 1
2 4 1
3 4 1
Sample Output:
2 4
题目大意：
给出N个城市，M条无向边。每个城市中都有一定数目的救援小组，所有边的边权已知。现在给出起点和终点，求从起点到终点的最短路径条数即最短路径上的救援小组数目之和。如果有多条最短路径，则输出数目之和最大的。

使用w[u]表示从起点s到达顶点u可以得到的最大点权之和，初始为0；num[u]表示从起点到u的最短路径条数，初始化时num[s]为1，其余num[u]均为0.接下来就可以在更新dis[v]时同时更新这两个数组

#include <iostream>
#include <vector>
using namespace std;
struct Edge
{
    int to ;
    int dis;
    int rescue;
    Edge(int _to,int _dis,int _rescue)
    {
        to = _to;
        dis = _dis;
        rescue  = _rescue;
    }
};
int rescue_num[505];//每个顶点救援小组数量
vector<Edge> graph[505];
bool vis[505] = {false};//是否遍历到
int dis[505] = {1000000000};//最短路径
int w[505] = {0};//最大点权和
int num[505] = {0};//最短路径条数
   int n,m,c1,c2;//点数 边数  开始 结束
void dj(int s)
{
    for(int i = 0 ;i < n ; i++)
    {
        dis[i] =1000000000;
    }
    dis[s] = 0;
    w[s] = rescue_num[s];
    num[s] =1;
    for(int i = 0 ; i< n ; i++)
    {
        int u  = -1 ; int min = 1000000000;
        for(int j = 0 ; j < n ; j++)
        {
            if(vis[j] == false && dis[j] <min)
            {
                u  = j ;
                min = dis[j];
            }
        }
        if(u == -1 )return;
        vis[u] = true;
        for(int v = 0 ; v< graph[u].size() ; v++)
        {
            Edge to =graph[u][v];
            if(vis[to.to] == false)
            {
                if(dis[to.to] > dis[u] + to.dis) //以u为中介点 能让d【v】更小
                {
                    //更新
                    dis[to.to] = dis[u] + to.dis;
                    w[to.to] = w[u] + rescue_num[to.to];
                    num[to.to] = num[u];
                }
                else if(dis[to.to] == dis[u] + to.dis)//以u为中介点 不能让d【v】更小
                {
                    if(w[to.to] < w[u] + rescue_num[to.to])//但是能让救援队数量更多 点权更大
                    {
                        w[to.to] = w[u] + rescue_num[to.to];//更新点权
                    }
                    num[to.to] += num[u];//只要有一条最短路，就加上
                }
                        
            }
        }
    }
    
    
}
int main(int argc, const char * argv[]) {
    cin>>n>>m>>c1>>c2;
    for(int i = 0 ; i < n ; i ++)
    {
        cin>>rescue_num[i];
    }
    int from ,to ,dis;
    for(int i = 0 ; i < m; i ++)
    {
        cin>>from;
        cin>>to;
        cin>>dis;
        graph[from].push_back(Edge(to,dis,rescue_num[from]));
        graph[to].push_back(Edge(from,dis,rescue_num[to]));
        
    }
    dj(c1);
    cout<<num[c2]<<" "<<w[c2]<<endl;
    return 0;
}

1013 Battle Over Cities (25分)（图的遍历）

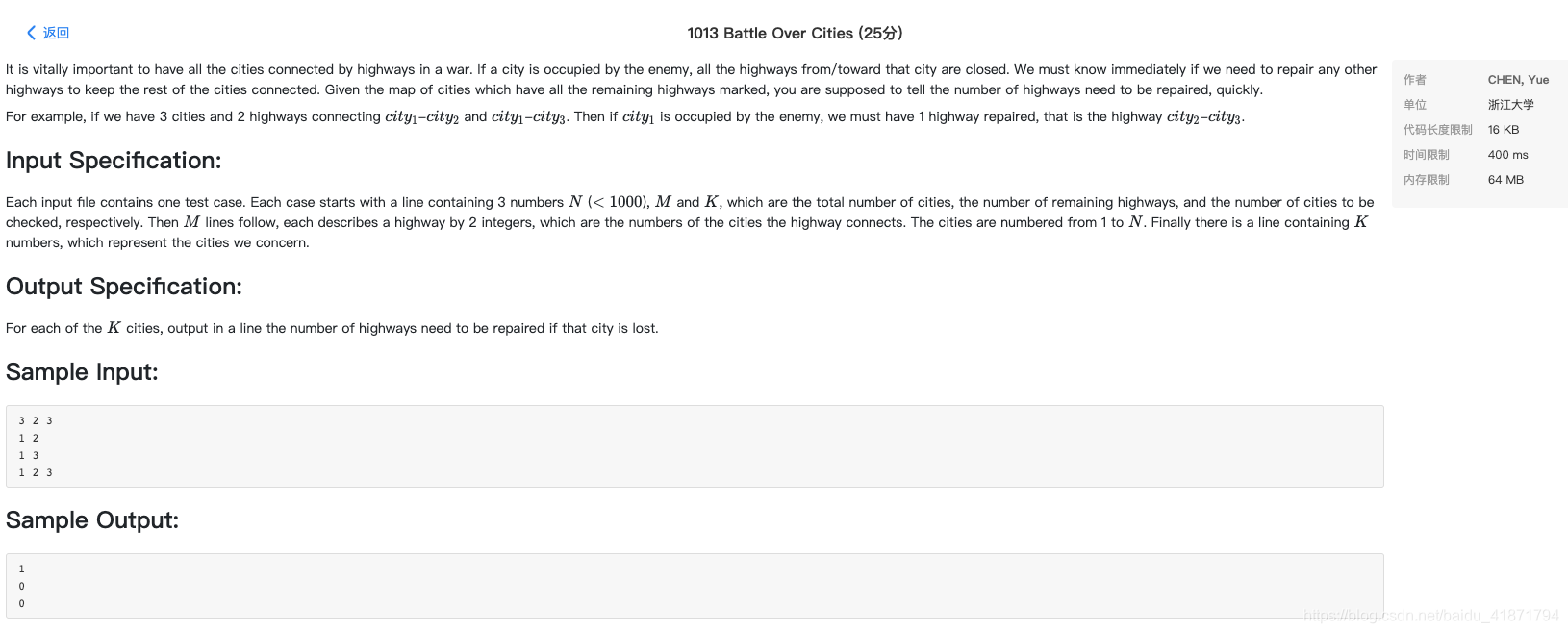
题目大意：给定一个无向图，并规定当删除某个顶点时，将会同时把与之连接的边一起删除。接下来给出k个查询，每个查询给出一个欲删除的顶点编号，求删除该顶点后需要增加多少边，才能使图变为连通（注：k次查询在原图上进行）

思路：
1.如何在给定无向图中，确定要增加的边，使得整个图连通。
假设无向图有n的连通分支（1，2，3…n）那么可以在1，2之间，2，3之间等等各加一条边，可使的整个无向图连通，这种做法需要添加的边应该是最少的。显然，需要添加的边等于连通块数-1。
2.此时问题转化成，求一个无向图的连通分支的数量，一般有两种方法，图的遍历和并查集。
（1）图的遍历：图的遍历过程中总是每次访问单个连通块，并将该连通块内的所有顶点都标记为已访问，然后去访问下一个连通块，因此可以在访问过程中同时计数遍历的连通块个数，就能得到需要添加的边数。
（2）并查集：判断无向图每条边的两个顶点是否在同一个集合内，如果在同一个集合内，则不作处理，如果不在一个集合内，则将这两个顶点加入同一个集合，最后统计有集合的个数。

• 方法一DFS：

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <string>
#include <map>
#include <vector>
using namespace std;
vector<int> graph[1010];
int vis[1010]  = {0};
int n,m,k;
int current;
void dfs(int i)
{
    if(i  == current)//到达已删除的顶点
        return;
    vis[i]=1;//标记此顶点已经被访问
    for(int j = 0 ; j <graph[i].size() ; j++)
    {
        if(vis[graph[i][j]] == 0)//如果找到未被访问的节点
        {
            dfs(graph[i][j]);//继续向下遍历
        }
    }       
}
int main(int argc, const char * argv[]) {
    // insert code here...
    
    scanf("%d%d%d",&n,&m,&k);
    //读入图数据
    for(int i = 0 ; i< m ; i++)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        graph[a].push_back(b);
        graph[b].push_back(a);     
    }
    //进行查询
    for(int query = 0 ; query < k ; query++)
    {
        scanf("%d",&current);//欲删除的顶点编号
        int block = 0;
        //每次遍历完成之后需要初始化vis数组
        for(int i = 0 ; i<1010 ; i ++)
        {
            vis[i] = 0;
        }
        for(int i = 1 ; i<= n ; i++)//枚举每个节点
        {
            if(i !=current && vis[i] == 0)//如果未被删除且未被访问
            {
                dfs(i);//遍历顶点i所在的连通分支
                block++;//连通分支数量+1
            }
        }
        printf("%d\n",block-1);
    }
    return 0;
}

• 方法二（并查集）：

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
#include <string>
#include <map>
#include <vector>
using namespace std;
int father[1010];
int vis[1010] = {0};
vector<int> graph[1010];
int n,m,k;
int current;
int findFather(int x)//查找x所在集合的根结点
{
    int a = x;
    while ( x != father[x]) {
        x =father[x];
    }
    while (a != father[a]) {
        int z = a;
        a = father[a];
        father[z] = x;
    }
    return x;
}
void Union(int a,int b)
{
    int fathera = findFather(a);
    int fatherb = findFather(b);
    if(fathera != fatherb)
    {
        father[fathera] = fatherb;
    }
}
// 初始化数组
void init()
{
    for(int i = 0 ; i<1010 ; i++)
       {
           father[i] = i;
           vis[i]  = 0;
       }
}
int main(int argc, const char * argv[]) {
    // insert code here...

 
    scanf("%d%d%d",&n,&m,&k);
    //读入图数据
    for(int i = 0 ; i< m ; i++)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        graph[a].push_back(b);
        graph[b].push_back(a);

    }
    //进行查询
    for(int query = 0 ; query < k ; query++)
    {
        scanf("%d",&current);//欲删除的顶点编号
        init();//每一次h循环结束，必须初始化
        for(int i = 1 ; i<= n ; i++)
        {
            for(int j = 0 ; j <graph[i].size() ; j++)// 遍历每条边
            {
                int u = i ;
                int v = graph[i][j];//边的两个端点
                if(u == current || v == current) continue;
                Union(u, v);//合并u v所在的集合
            }
        }
        int block = 0;//连通分支个数
        for(int i = 1 ; i<= n ; i++) //遍历所有节点
              {
                  if(i == current) continue;
                  int fa_i = findFather(i);//顶点i所在的连通块的根结点为fa_i
                  if(vis[fa_i] == false)//如果当前连通块的根结点未被访问
                  {
                      block++;//连通块e个数+1
                      vis[fa_i] = true;//当前连通块的根结点设为已访问
                  }
              }
  
        printf("%d\n",block-1);
    }
    return 0;
}