强化学习基础理论

强化学习基础理论。强化学习（Reinforcement learning），与监督学习，无监督学习是类似的，是一种统称的学习方式。它主要利用智能体与环境进行交互，从而学习到能获得良好结果的策略。与有监督学习不同，强化学习的动作并没有明确的标注信息，只有来自环境的反馈的奖励信息，它通常具有一定的滞后性，用于反映动作的“好与坏”。

知识结构

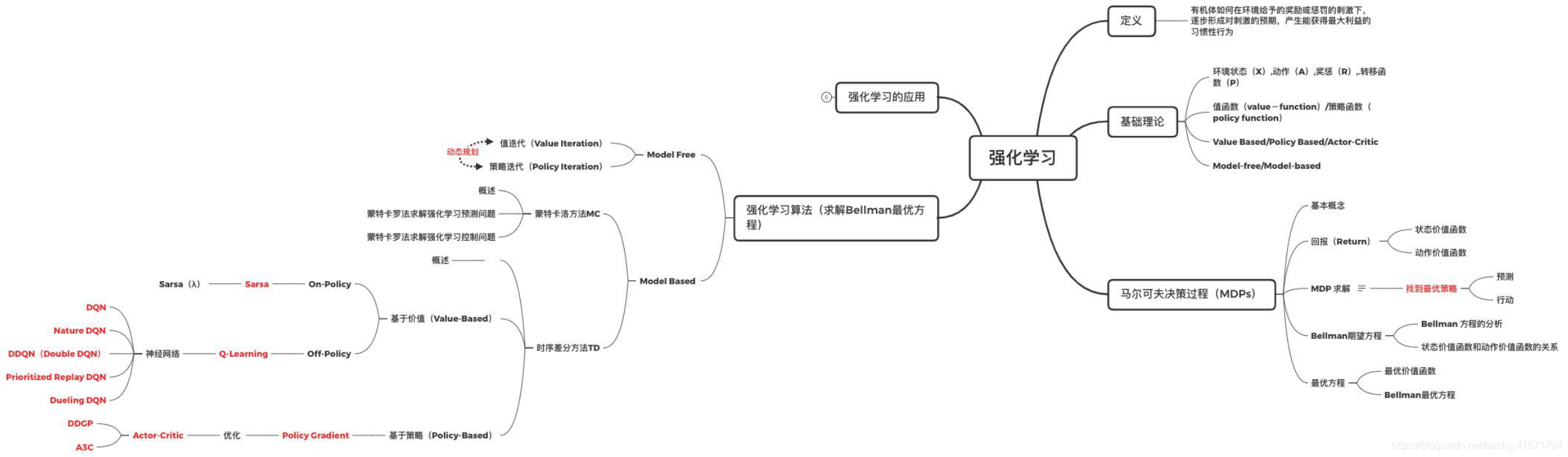
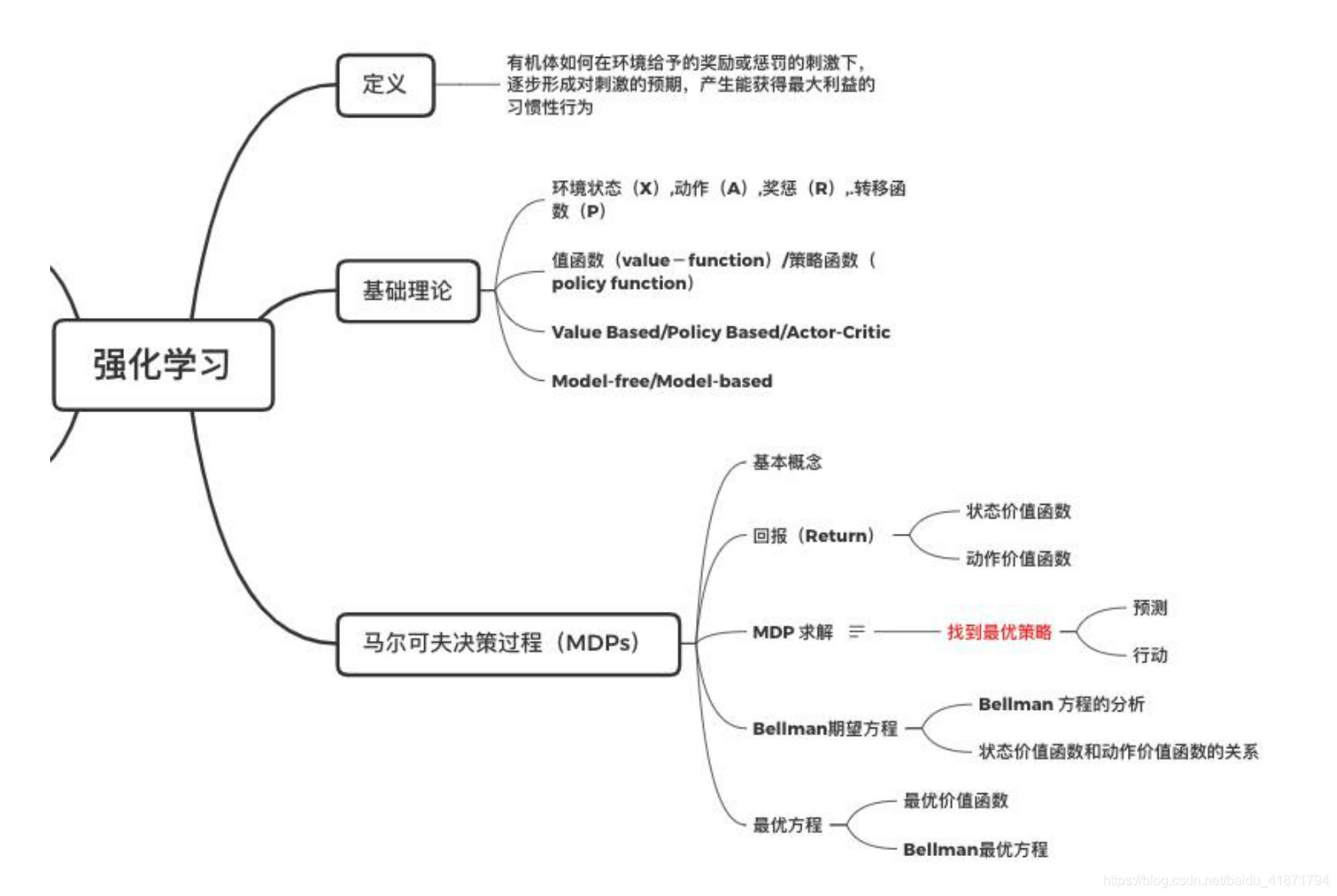
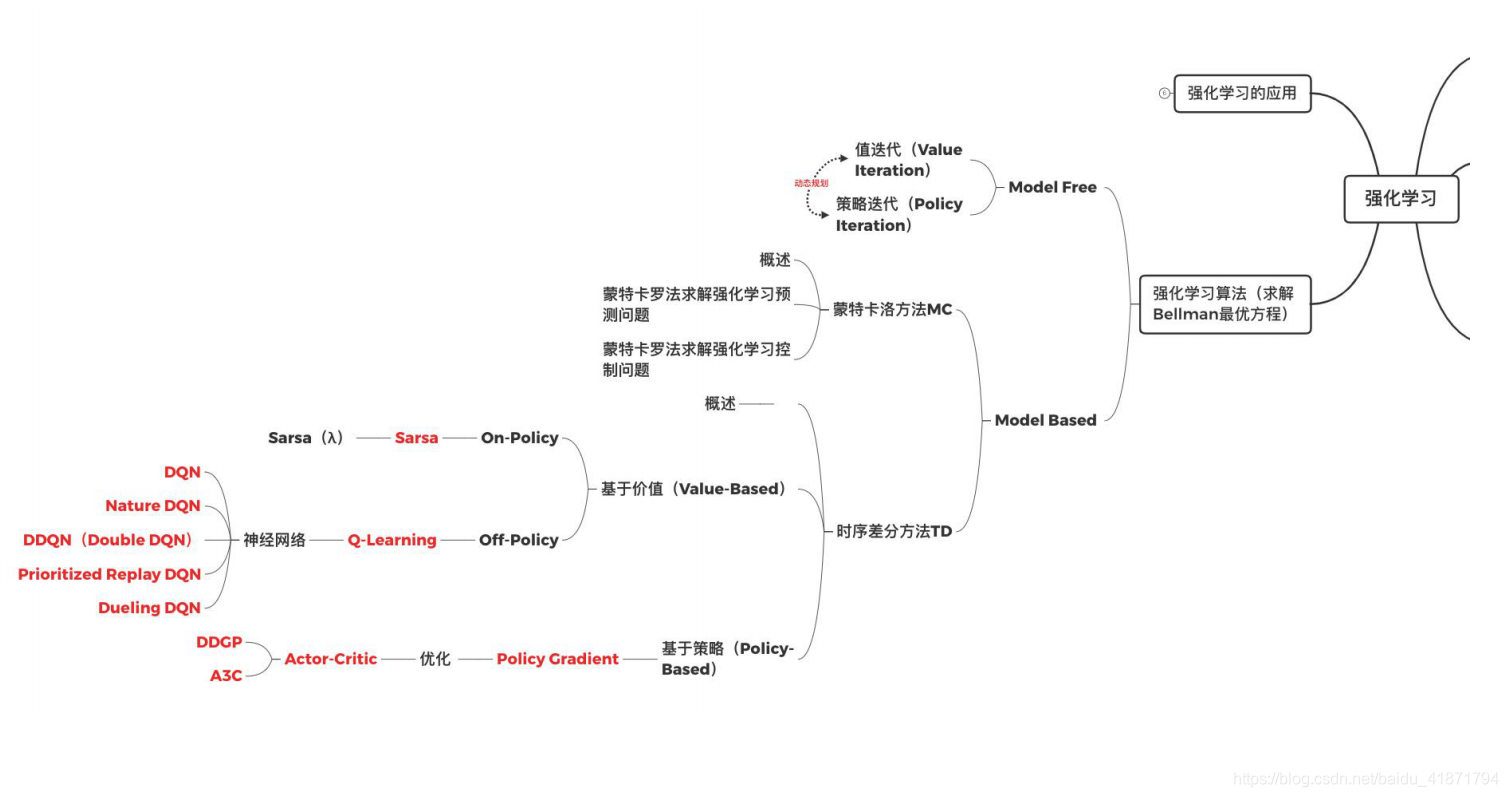
定义

强化学习（Reinforcement learning），与监督学习，无监督学习是类似的，是一种统称的学习方式。它主要利用智能体与环境进行交互，从而学习到能获得良好结果的策略。与有监督学习不同，强化学习的动作并没有明确的标注信息，只有来自环境的反馈的奖励信息，它通常具有一定的滞后性，用于反映动作的“好与坏”。

参考资料：
https://zh.wikipedia.org/wiki/强化学习

基础理论

基本概念

• 4 个主要概念：环境状态（S）、动作（A）和奖惩（R）， 转移函数（P）。
  机器感知到的环境描述构成环境状态（S），机器采取的动 作构成了动作空间（A），潜在的转移函数（P）使环境从当前 的状态转移到另一个状态，在转移到另一个状态的同时，环境根据潜在的奖励函数（R）反馈给机器一个奖赏。（遵循马尔可夫 决策过程 MDP）。

• 环境状态（S）：反映了环境的状态特征，在时间戳𝑡上的状态记为𝑠𝑡，它可以是原始的视觉图 像、语音波形等信号，也可以是高层抽象过后的特征，如小车的速度、位置等数据， 所有的(有限)状态构成了状态空间𝑆。

• 动作（A）：智能体采取的行为，在时间戳𝑡上的状态记为𝑎𝑡，可以是向左、向右等离散动 作，也可以是力度、位置等连续动作，所有的(有限)动作构成了动作空间𝐴。

• 策略𝜋(𝑎|𝑠)：代表了智能体的决策模型，接受输入为状态𝑠，并给出决策后执行动作的 概率分布𝑝(𝑎|𝑠)，满足
  
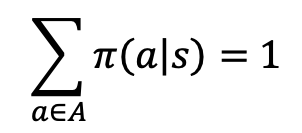
  这种具有一定随机性的动作概率输出称为随机性策略(Stochastic Policy)。特别地，当 策略模型总是输出某个动作的概率为 1，其它为 0 时，这种策略模型称为确定性策略 (Deterministic Policy)，即𝑎 = 𝜋(𝑠)

• 奖励𝑟(𝑠, 𝑎)：表达环境在状态𝑠时接受动作𝑎后给出的反馈信号，一般是一个标量值，它在一定程度上反映了动作的好与坏，在时间戳𝑡上的获得的激励记为𝑟t(部分资料上记为r（t+1） ，这是因为激励往往具有一定滞后性)

• 状态转移概率𝑝(𝑠′|𝑠, 𝑎) ：表达了环境模型状态的变化规律，即当前状态𝑠的环境在接受动作𝑎后，状态改变为𝑠′的概率分布，满足
  
  

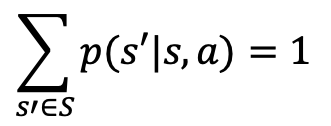
• 在环境重的状态转移，奖赏的返回不受机器控制，机器只能 选择所做的动作来影响环境，通过观察转移后的状态和返回的奖 赏感知环境。机器只能通过在环境中不断尝试，学得一个策略， 根据策略就可以知道在某个状态下执行什么动作可以得到最多的奖赏。

• 目标：模型要在训练的过程中不断作出尝试性的决策，错了 就惩罚，对了就奖励，找到能使长期积累奖赏最大化的策略。

• 值函数（value－function）：在我们目前的环境（environment） 中首先找到最有价值的状态 states。根据它就可以朝着奖励值增 加的状态方向运动，因此得到各个状态下的决策，将所有的策略都计算在内求出来的一个期望的奖励值(Return)。

• 策略函数（policy function）：一个从状态到动作的映射 是根据价值函数选择产生最大奖励的行动的一组策略，告诉智能 体如何挑选下一个动作。

• Value Based：学习值函数，隐含策略函数

• Policy Based：不学习值函数，只学习策略函数

• Actor-Critic：同时学习值函数和策略函数

Model-free 和 Model-based

• （1）Model-based RL：让 agent 学习一种模型，这种模型能 够从它的观察角度描述环境是如何工作的，然后利用这个模型做出动作规划，具体来说，当 agent 处于 s1 状态，执行了 a1 动作， 然后观察到了环境从s1转化到了s2以及收到的奖励 r,那么这些 信息能够用来提高它对 T(s2|s1,a1)和 R(s1,a1)的估计的准确性，当 agent学习的模型能够非常贴近于环境时，它就可以直接通过一 些规划算法来找到最优策略，具体来说：当 agent 已知任何状态下执行任何动作获得的回报，即 R(st,at）已知，而且下一个状态 也能通过T(st+1|st,at)被计算，那么这个问题很容易就通过动态规 划算法求解，尤其是当 T(st+1|st,at)＝1时，直接利用贪心算法， 每次执行只需选择当前状态 st 下回报函数取最大值的动作 maxaR(s,a|s=st)即可，

• （2）Model-free RL：我们有时候并不需要对环境进行建模 也能找到最优的策略，一种经典的例子就是 Q-learning，Q-learning 直接对未来的回报 Q(s,a)进行估计，Q(sk,ak)表示对 sk 状态下执行动作 at 后获得的未来收益总和 E(∑nt=kγkRk)的估 计，若对这个 Q 值估计的越准确，那么我们就越能确定如何选 择当前 st 状态下的动作：选择让Q(st,at)最大的 at 即可，而 Q 值 的更新目标由Bellman方程定义，更新的方式可以有TD（Temporal Difference 时间差分）等，这种是基于值迭代的方法，类似的还有基于策略迭代的方法以及结合值迭代和策略迭代的actor-critic 方法，基础的策略迭代方法一般回合制更新（Monte Carlo Update蒙特卡洛学习），这些方法由于没有去对环境进行建模，因此他 们都是 Model-free 的方法。

• （3）如果你想查看这个强化学习算法是 model-based 还是 model-free 的，你就问你自己这个问题：在 agent执行它的动作 之前，它是否能对下一步的状态和回报做出预测，如果可以，那 么就是 model-based 方法，如果不能，即为model-free 方法.

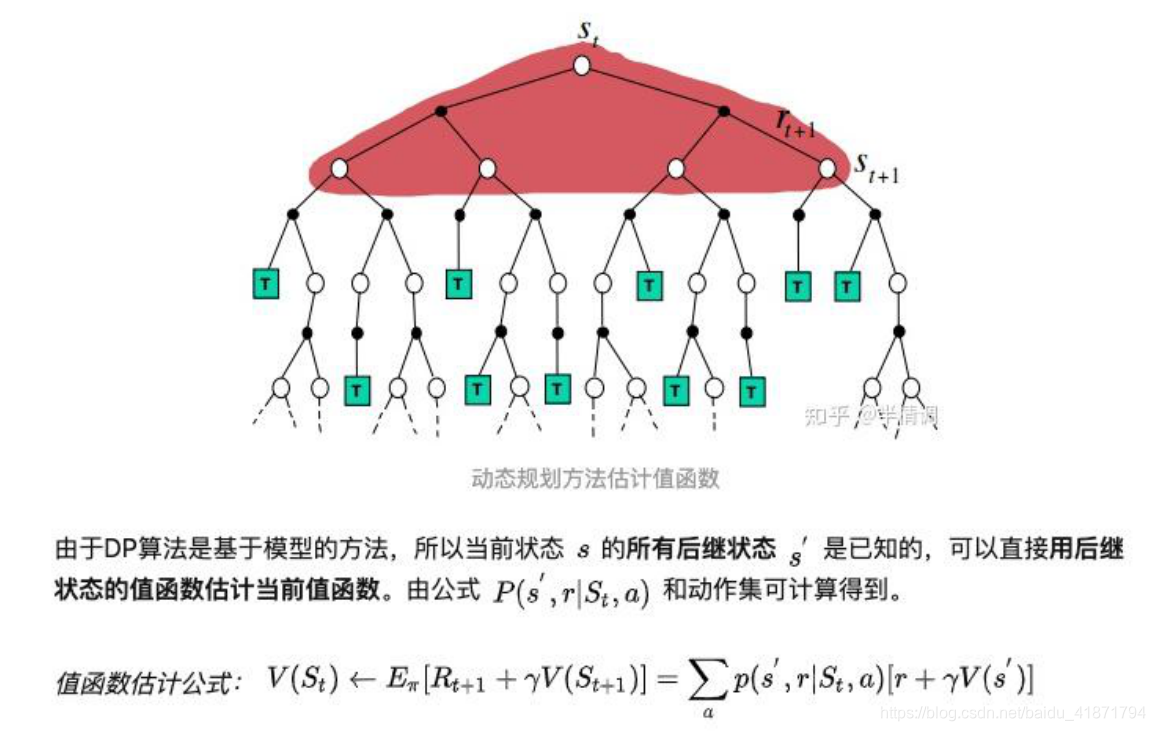
• (4)如果能够获得环境的状态转移概率𝑝(𝑠′|𝑠, 𝑎)和激励函数𝑟(𝑠, 𝑎)，可以直接迭代计算值函数，这种已知环境模型的方法统称为基于模型的强化学习(Model-based Reinforcement Learning)。然而现实世界中的环境模型大都是复杂且未知的，这类模型未知的方法统称为 模型无关的强化学习(Model-free Reinforcement Learning)，接下来我们主要介绍模型无关的强化学习算法。
  

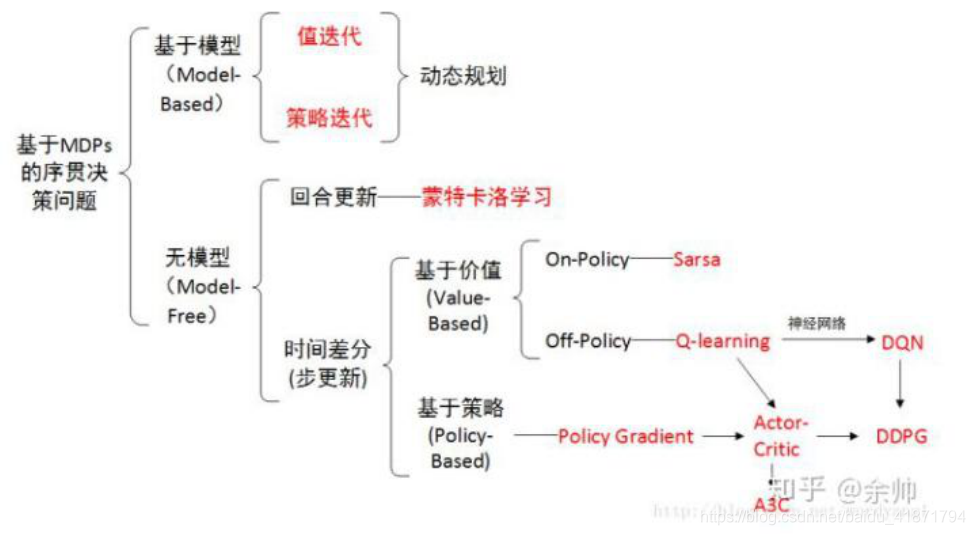
参考资料：
https://zhuanlan.zhihu.com/p/40118471
https://zhuanlan.zhihu.com/p/36494307

马尔可夫决策过程（Markov Decision Processes,MDPs）

参考资料：https://zhuanlan.zhihu.com/p/25319023

基本概念

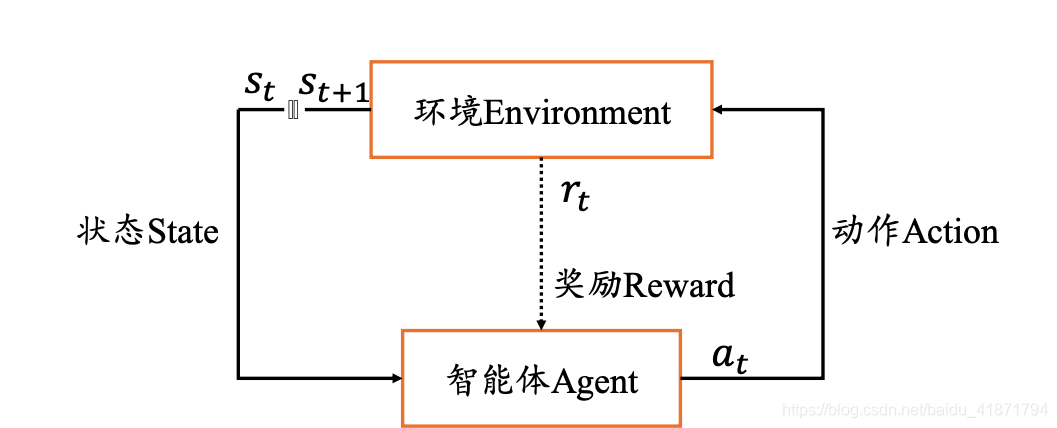
• MDPs 简单说就是一个智能体（Agent）采取行动（Action） 从而改变自己的状态（State）获得奖励（Reward）与环境 （Environment）发生交互的循环过程。
• MDP 的策略完全取决于当前状态（Only present matters），这也是它马尔可夫性质的体现。其可以简单表示为：
  
  

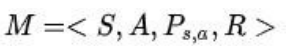
回报（Return）：

MDP 求解

• （1）预测：给定策略，评估相应的状态价值函数和状态-动作价值函数
• （2）行动：根据价值函数得到当前状态对应的最优动作

Bellman 期望方程

• Bellman 方程的分析

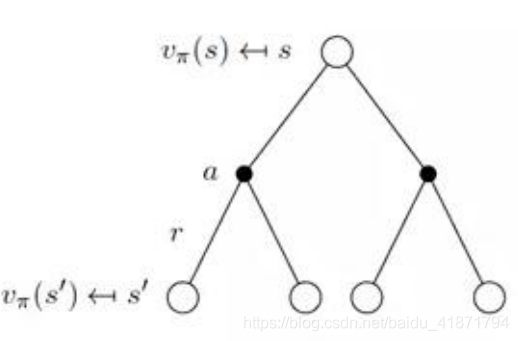
第一层的空心圆代表当前状态（state），向下连接的实心圆代表当前状态可以执行两个动作，第三层代表执行完某个动作后可能到达的状态 s’。

状态价值函数：

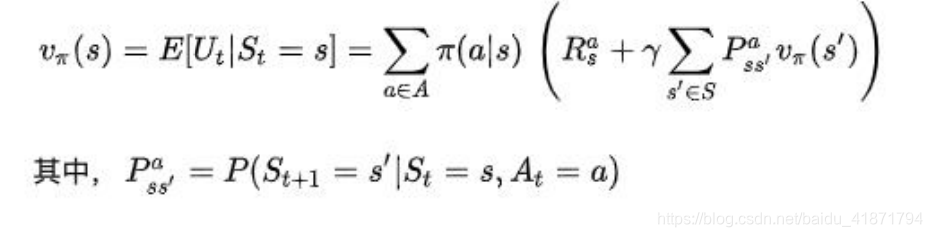
解释：策略π是指给定状态 s 的情况下，动作 a 的概率分 布，即 π（a | s) = P（a | s) .

将概率和转换为期望:

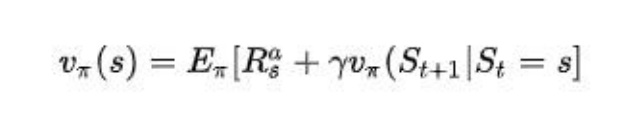
动作价值函数:

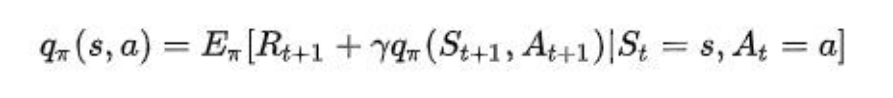
• 状态价值函数和动作价值函数的关系

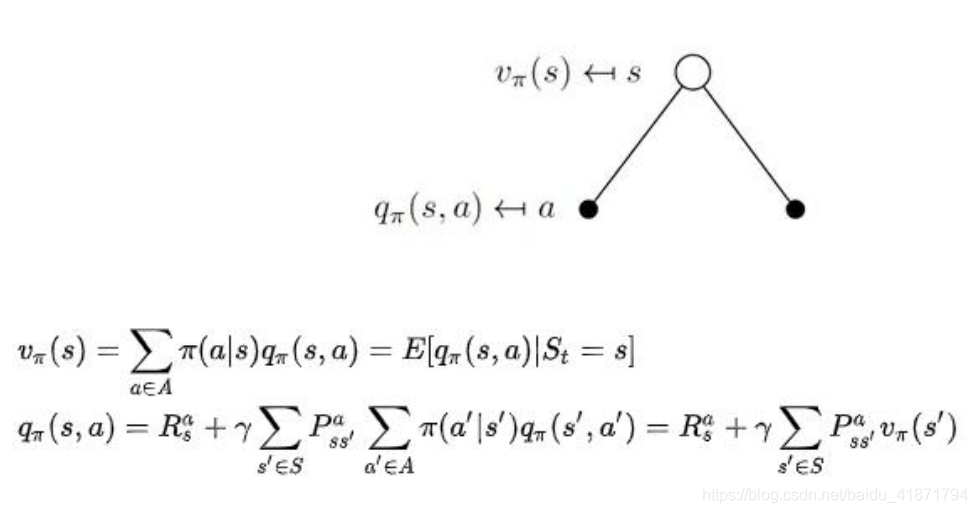
（1）V(s）代表 t 时刻状态 s 能获得的回报，他是 s 状态能执行的 所有 action 的概率乘以每个动作得到的回报的和。

（2）Q(s,a)表示基于 t 时刻的状态 s，选择一个 action 后能获得的未 来回报（return）的期望。等于在状态 s 时采取动作a 的奖励加 上有 s 转移到 s’（基于概率 P）后在 s’执行他对应的所有动作a’的回报和，不断向下传递，参数Υ为折扣因子，代表距离现 在越遥远的奖励不如现在的奖励大。

最优方程

• 最优价值函数（optimal state-value function）
  所有策略下价值函数的最大值：
  
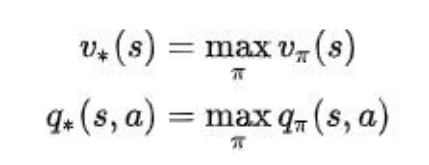
• Bellman 最优方程
  

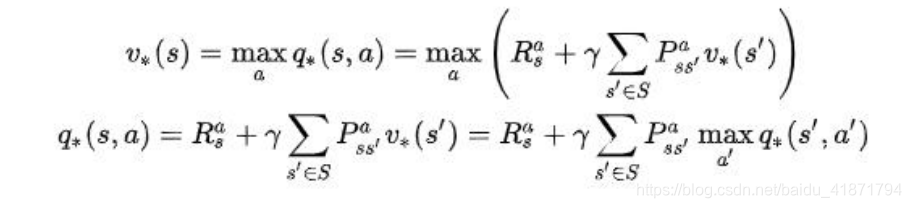
（1）v 描述了处于一个状态的长期最优化价值，即在这个状态下考虑到所有可能发生的后续动作，并且都挑选最优的动作来执行的情况下，这个状态的价值 。
（2）q 描述了处于一个状态并执行某个动作后所带来的长期最优价值，即在这个状态下执行某一特定动作后，考虑再之后所有可能处于的状态并且在这些状态下总是选取最优动作来执行所带来的长期价值。

强化学习算法（求解 Bellman 最优方程）

Model Free RL 算法（动态规划求解 MDPs）

• 概述
  MDP 的某一时刻的子问题仅仅取决于上一时刻的子问题的 action，并且 Bellman 方程可以递归地切分子问题，所以我们可以采用动态规划来求解 Bellman 方程。
  MDP 的问题主要分两类：
  （1）Prediction 问题：
  
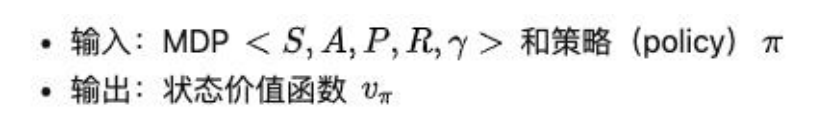
  给定强化学习的 6 个要素：状态集 S, 动作集 A, 模型状态转化概率矩阵 P, 即时奖励 R，衰减因子γ, 给定策略π， 求解该策略的状态价值函数 v（π）
  （2）Control 问题：
  
  求解最优的价值函数和策略。给定强化学习的5个要素：状态集S, 动作集A, 模型状态转化概率矩阵 P, 即时奖励 R，衰减 因子γ, 求解最优的状态价值函数 v∗和最优策略π∗。
• Policy Iteration （策略迭代）
  
  公式理解：在当前状态 s 下，可以执行的动作集合 A 中的每一个 动作 a 执行的概率和预期回报乘积之和。
  
• Value Iteration（值迭代）
  
• 总结
  （1）迭代策略评估（Iterative Policy Evaluation）解决的是 Prediction 问题，使用了贝尔曼期望方程（Bellman Expectation Equation） （2）策略迭代（Policy Iteration）解决的是 Control 问题，实 质是在迭代策略评估之后加一个选择 Policy 的过程，使用的是贝尔曼期望方程和贪心算法 。
  （3）价值迭代（Value Iteration） 解决的是 Control 问题， 它并没有直接计算策略（Policy），而是在得到最优的基于策略 的价值函数之后推导出最优的 Policy，使用的是贝尔曼最优化方 程（Bellman Optimality Equation）。
  

蒙特卡洛方法 MC （Model Based RL）

• 概述
  （1）蒙特卡罗法通过采样若干经历完整的状态序列(episode)来估 计状态的真实价值。所谓的经历完整，就是这个序列必须是达到 终点的。比如下棋问题分出输赢，驾车问题成功到达终点或者失 败。有了很多组这样经历完整的状态序列，我们就可以来近似的 估计状态价值，进而求解预测和控制问题了。
  （2）从特卡罗法法的特点来说，一是和动态规划比，它不需要依 赖于模型状态转化概率。二是它从经历过的完整序列学习，完整 的经历越多，学习效果越好。
  
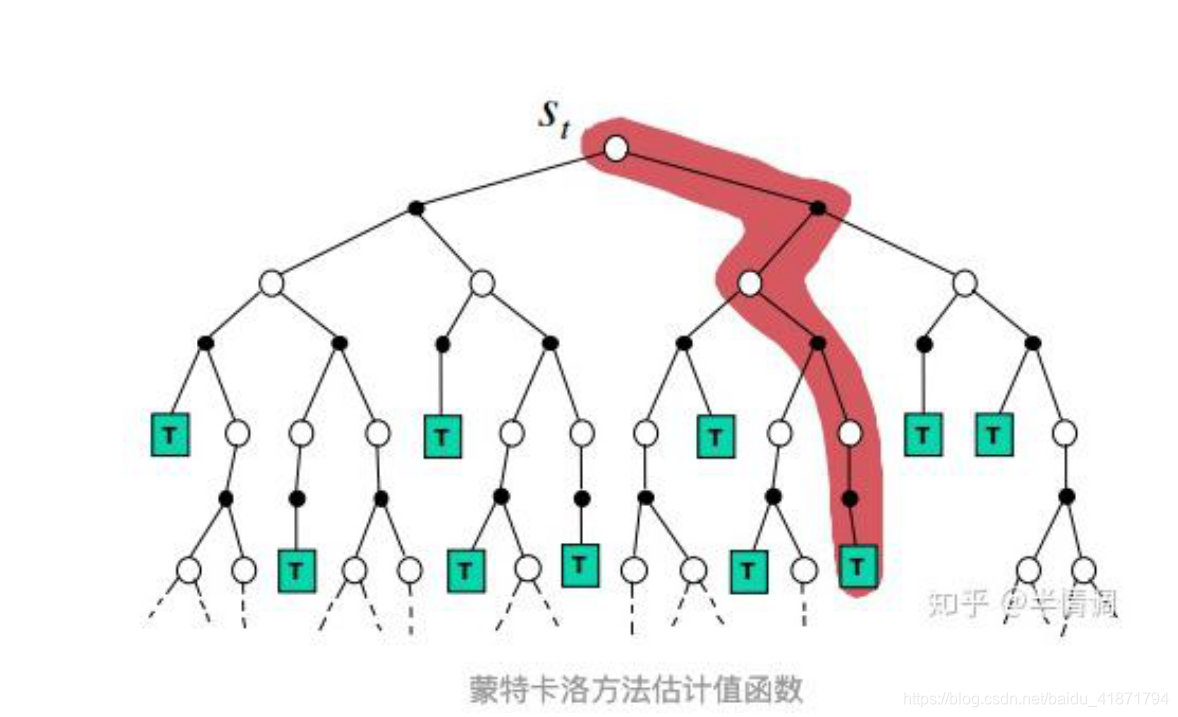
  （3）由于没有模型，后继状态无法全部得到，所以 MC 方法利用 经验平均估计状态的值函数，要等一次试验经历后才能知道。相 对于动态规划方法，学习速度慢，效率低。
  值函数估计公式：
  
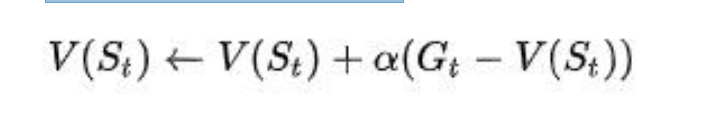
• 蒙特卡罗法求解强化学习预测问题（Prediction问题）
  
  
• 蒙特卡罗法求解强化学习控制问题
  
  
• 总结
  蒙特卡罗法是一种不基于模型的强化问题求解方法。它可以 避免动态规划求解过于复杂，同时还可以不事先知道环境转化模 型，因此可以用于海量数据和复杂模型。但是它也有自己的缺点， 这就是它每次采样都需要一个完整的状态序列。如果我们没有完 整的状态序列，或者很难拿到较多的完整的状态序列，这时候蒙 特卡罗法就不太好用了。

参考资料：https://www.cnblogs.com/pinard/p/9492980.html

时序差分方法 TD（Model Based RL）

• 概述
  
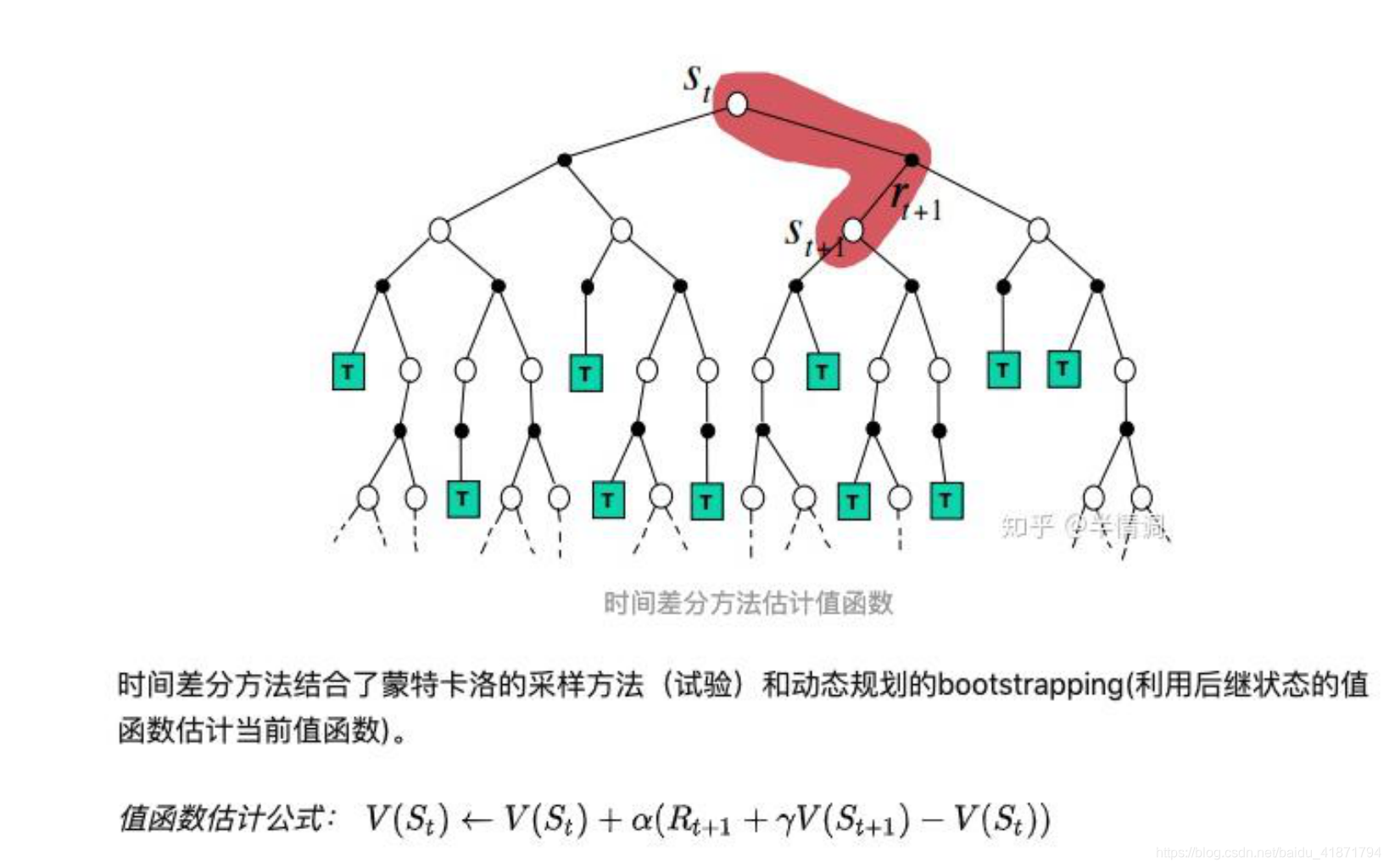
  对于时序差分法来说，我们没有完整的状态序列，只有部分的状态序列。
  贝尔曼方程：
  
• 时序差分TD的预测问题求解
  
• 蒙特卡罗法和时序差分法求解预测问题的区别
  （1）时序差分法在知道结果之前就可以学习，也可以在没 有结果时学习，还可以在持续进行的环境中学习，而蒙特卡罗法 则要等到最后结果才能学习，时序差分法可以更快速灵活的更新 状态的价值估计，这在某些情况下有着非常重要的实际意义。
  （2）时序差分法在更新状态价值时使用的是 TD 目标值， 即基于即时奖励和下一状态的预估价值来替代当前状态在状态 序列结束时可能得到的收获，是当前状态价值的有偏估计，而蒙 特卡罗法则使用实际的收获来更新状态价值，是某一策略下状态 价值的无偏估计，这一点蒙特卡罗法占优。
  （3）虽然时序差分法得到的价值是有偏估计，但是其方差 却比蒙特卡罗法得到的方差要低，且对初始值敏感，通常比蒙特 卡罗法更加高效。
  （4） 时序差分法的优势比较大，因此现在主流的强化学习求解方 法都是基于时序差分的。
• 时序差分的控制问题求解
  （1）离线控制(off-policy) Q-Learning
  （2）在线控制(on-policy) SARSA

Q-Learning（Value-Based 与 Off-Policy）

一个基于值的强化学习算法，利用 Q 函数寻找最优的（动作—选择）策略。

• 基本概念：
  （1）Q-Table：一个表格，给出了每一个状态（state）上进 行的每一个动作（action）计算出最大的未来奖励（reward）的期 望。（Q-Table 的初始值在探索环境之前任意设定（大多数情况 下是 0），随着对环境的持续探索，Q-Table中的值会被不断的更新，给出越来越好的近似）
  （2）学习动作值函数（action value function）：动作值函数（或称「Q 函数」）有两个输入：「状态」和「动作」。它将返回在该状态下执行该动作的未来奖励期望。
  
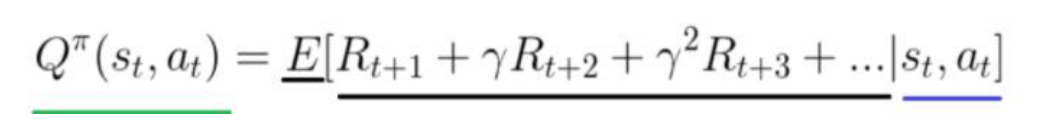
  Q 函数视为一个在 Q-table 上滚动的读取器，用于寻找与当前 状态关联的行以及与动作关联的列。它会从相匹配的单元格中返 回 Q 值。这就是未来奖励的期望。
• Q-Learning 算法流程
  
  （1）初始化 Q-Table，构造了一个 m 列（m = 动作数 )，n 行 （n = 状态数）的 Q-table，并将其中的值初始化为 0。
  （2）在整个生命周期中，步骤 3 到步骤 5 会一直被重复， 直到达到了最大的训练次数（由用户指定）或者手动中止训练。
  （3）选取一个动作。在基于当前的 Q 值估计得出的状态 s 下 选择一个动作 a。 在这个过程中使用ϵ-greedy 策略：我们会以ϵ的概率随机选 择一个动作，以 1-ϵ的概率按照 Q-Table 进行动作的选择。（由于初始状态 Q-Table 基本为 0，所以初始时的ϵ应该为 1，然后随 着迭代次数的不断增加，逐渐减小ϵ的值）
  （4）评价，采用动作 a 并且观察输出的状态 s’ 和奖励 r。 现在我们更新函数 Q（s，a），我们采用在步骤 3 中选择的动作 a，然后执行这个动作会返回一个新的状态 s’ 和奖励 r，我 们对 Q（s，a）进行更新。
  
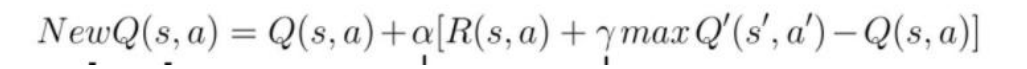
  Q（s，a）现实=R（s,a）+Υ*maxQ（s’，a’）
  Q（s，a）估计 = Q（s，a）
  Alpha 为学习率
• 总结
  （1）它根据动作值函数评估应该选择哪个动作，这个函数决 定了处于某一个特定状态以及在该状态下采取特定动作的奖励 期望值。
  （2）目的：最大化 Q 函数的值（给定一个状态和动作时的 未来奖励期望）
  （3）函数 Q（state，action）→返回在当前状态下采取该动作 的未来奖励期望。
  （4）在我们探索环境之前：Q-table 给出相同的任意的设定值 → 但是随着对环境的持续探索→Q 给出越来越好的近似。
  （5）下一个动作 a 的选择标准是要能够最大化下一个状态的 Q （St+1，a）值（贪心策略），而不是遵循当前的策略。因此， Q-Learning 属于离策略（off-policy）算法。

参考资料：https://www.jiqizhixin.com/articles/2018-04-17-3 https://www.jiqizhixin.com/articles/2018-04-17-3

Sarsa 算法（State-Action-Reward-State-Action）

Sarsa 很像 Q-learning。SARSA 和 Q-learning 之间的关键区 别是 SARSA 是一种在策略（on-policy）算法。这意味着 SARSA 根据当前策略执行的动作而不是贪心策略来学习Q值。

• 算法思想
  其学习更新函数依赖的 5 个值，分别是当前状态 S1，当前状 态选中的动作A1，获得的奖励 Reward，S1 状态下执行 A1 后取得的状态 S2 及 S2 状态下将会执行的动作 A2。
  
  
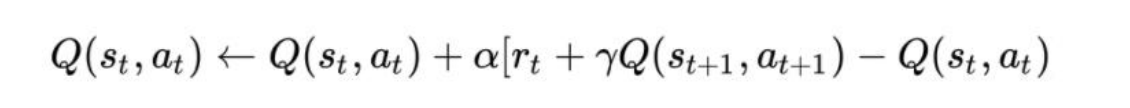
  （1）折扣系数Υ，决定了未来奖励的重要性。Υ为 0 时，会让 变得 “机会主义”，只会考虑目前的奖励，而当 Gamma 接近 1 时， 会争取长期高回报。
  （2）假定初始条件。一个低 (无限) 初始值，也被称为 “乐观初 始条件”，可以鼓励探索。无论发生什么行动, 更新规则导致它具 有比其他替代方案更高的价值，从而增加他们的选择概率。
  （3）SarSa 中使用ϵ−greedy（ϵ的概率随机选择，1-ϵ的按照规定 选择）策略生成 action a，随即又用 a 处对应的值函数来计算 target，更新上一步的值函数。所以 SarSa 是一种 off-policy 算法。

Sarsa(lambda)算法

Sarsa(lambda)算法是 Sarsa 的改进版，二者的主要区别在于： 在每次 take action 获得 reward 后，Sarsa 只对前一步 Q(s,a)进 行更新，Sarsa(lambda) 则会对获得 reward 之前的步进行更新。

Sarsa(lambda)算法中多了一个矩阵E(eligibility trace)，它是用来保存在路径中所经历的每一步，因此在每次更新时也会对之前 经历的步进行更新。

参考资料：https://blog.csdn.net/u010089444/article/details/80516345

Deep Q Network（DQN）算法（NIPS 2013）

• 概述
  （1）当状态和动作空间是高维连续时，Q-Table 存储状态对应动 作的奖赏值十分困难，耗费空间非常庞大，而 DQN 融合了神经 网络和 Q-Learning 的算法，将 Q-table 更新转化为一种函数拟合 问题，通过拟合函数，使得相近的状态得到相近的输出动作。
  （2）值函数近似：一个状态-动作会对应一个值函数 Q（s,a）， 理论上对于任意的(s,a)我们都可以由公式求出它的值函数（查询 Q-Table），但是维度很高的情况下，Q-Table 会变得很大，查询 效率很低，所以可以用函数近似的方式去估计值函数： Q（s，a，ω）≈ Q（s，a）（其中ω可以是通过 DQN 学习到的 神经网络的参数）
  （3）DQN 是一种 value based 算法，这种算法中只有一个值函数 网络，没有 policy 网络。
• 算法原理
  （1）DQN 用神经网络来拟合值函数进行值函数近似估计，神经网络可以输入当前的状态 state。通过神经网络计算出值函数后，输出对应的 action。
  
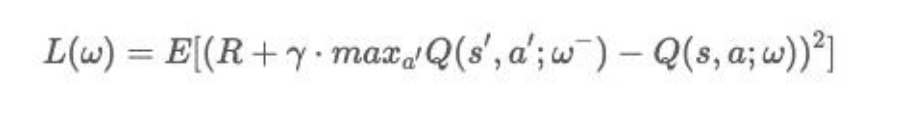
  （2）这个损失函数求了真实值与预测值的差的平方和，预测值是 神经网络的输出 Q(s,a;w)，而真实值则不好估计，由于没有存储 Q-Table，则无法查表得到真实的奖励值。
  假如想求出从状态 state 出发，并采取动作 action 的话，可 以得到整体收益的期望值 Q(s,a)的话，有两种情况：
  ①Model Based RL：我们知道环境的模型，即存储了 Q-Table： 当处于(s,a)时，下一个到达的状态可能是什么，并且到达每一个 状态的概率是什么；我们还知道奖励函数：当处于(s,a)时，得到 的立即回报的期望值是什么；有了这两个信息，我们可以通过马 尔可夫决策过程的贝尔曼方程求解出最优策略。
  ②Model Free RL：不使用环境模型（没有 Q-Table），使用 采样的方法得到真实值，具体的方法有 Monte Carlo，Temporal Difference / SarSa。
  （3）DQN 属于 Model Free 的强化学习算法，他需要进行采样， 例如使用上面介绍的 Q-Learning，利用下一个 step 来更新值函 数。
  
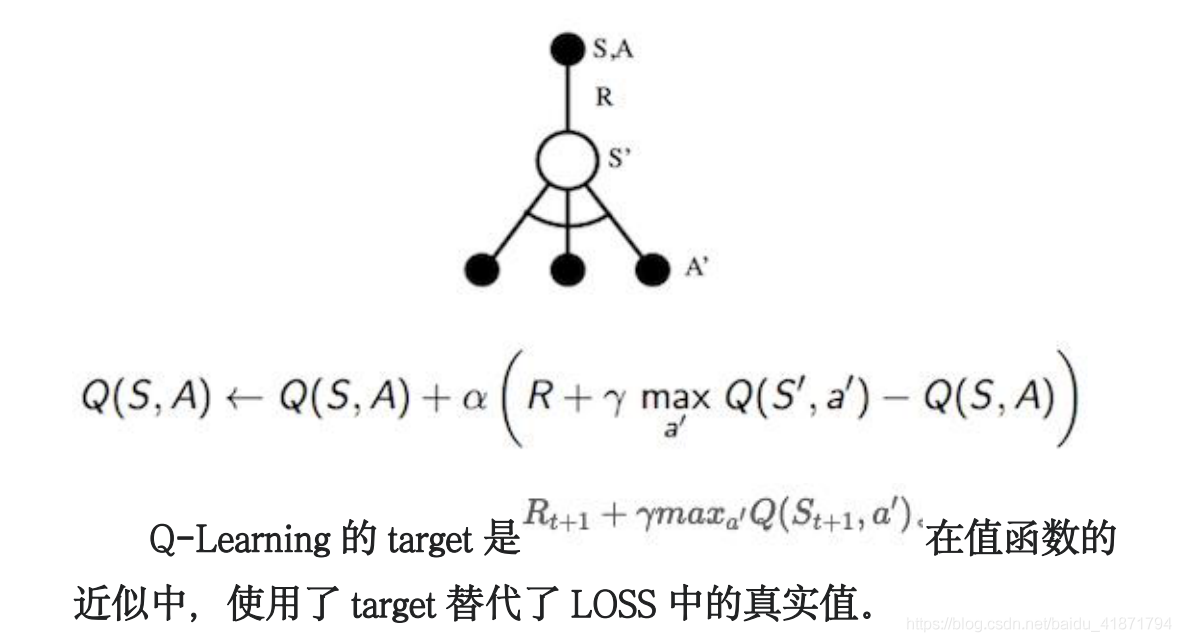
• DQN的改进
  （1）DQN 也是一种 Off-policy 的算法，但是 Q-Learning 中用来计 算 target 和预测值的函数 Q 是同一个函数 Q，也就是说使用了相 同的神经网络。这样带来的一个问题就是，每次更新神经网络的时候，target 也都会更新，这样会容易导致参数不收敛。（在监督学习中，label 都是固定的，不会根据神经网络参数的改变而改变）。
  （2）解决方法是 DQN 在原来的 Q 网络的基础上又引入了一个 target Q 网络，即用来计算 target 的网络。它和 Q 网络结构一样， 初始的权重也一样，只是 Q 网络每次迭代都会更新，而 target Q 网络是每隔一段时间才会更新。DQN 的 target是
  
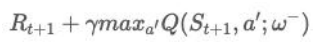
  用 ω−表示它比 Q 网络的权 重 ω更新得要慢一些。
  （3）经验回放 Experience replay：由于在强化学习中，我们得到 的观测数据是有序的，用这样的数据去更新神经网络的参数会有 问题（对比监督学习，数据之间都是独立的）。因此 DQN 中使 用经验回放，即用一个 Memory 来存储经历过的数据，每次更新 参数的时候从 Memory 中抽取一部分的数据来用于更新，以此来 打破数据间的关联。
• 算法流程
  
  原文的算法流程：
  

参考资料：https://zhuanlan.zhihu.com/p/21421729
https://wanjun0511.github.io/2017/11/05/DQN/
https://blog.csdn.net/kenneth_yu/article/details/78478356

Nature DQN

• 概述
  在上面的 DQN 中，我们可以看到在计算目标值 yj 时和计算 当前值用的是同一个网络 Q，这样在计算目标值 yj 时用到了我们 需要训练的网络 Q，之后我们又用目标值 yj 来更新网络 Q 的参 数，这样两者的依赖性太强，不利于算法的收敛，因此在 Nature DQN 中提出了使用两个网络，一个原网络 Q 用来选择动作，并 更新参数，另一个目标网络 Q′只用来计算目标值 yj，在这里目 标网络 Q′的参数不会进行迭代更新，而是隔一定时间从原网络Q 中复制过来，因此两个网络的结构也需要完全一致，否则无法 进行参数复制。
• 算法思想
  （1）Nature DQN 使用了两个 Q 网络，一个当前 Q 网络 Q 用来选 择动作，更新模型参数，另一个目标 Q 网络′Q′用于计算目标 Q 值。目标 Q 网络的网络参数不需要迭代更新，而是每隔一段时 间从当前 Q 网络 Q 复制过来，即延时更新，这样可以减少目标 Q 值和当前的 Q 值相关性。
  （2）两个 Q 网络的结构是一模一样的。这样才可以复制网络参数。
  （3）Nature DQN 和 DQN 相比，除了用一个新的相同结构的目标Q网络来计算目标Q值以外，其余部分基本是完全相同的。
  （4）算法流程来自 DQN NIPS 2015：

（5）Nature DQN 与 DQN 的不同之处在于：
有两个网络 Q 和 Q’，分别对应不同的参数。
还有就是更改目标值的公式不同：

参考资料：https://www.cnblogs.com/jiangxinyang/p/10112381.html

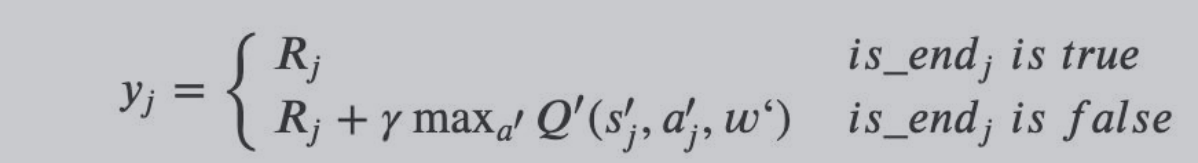
DDQN（Double DQN）

• 概述
  在 DDQN 之前，基本上所有的目标 Q 值都是通过贪婪法直接得 到的，无论是 Q-Learning 还是 DQN(NIPS 2013)。使用 max 虽然 可以快速让 Q 值向可能的优化目标靠拢（注：对于真实的策略 来说并在给定的状态下并不是每次都选择使得 Q 值最大的动作， 因为一般真实的策略都是随机性策略，所以在这里目标值直接选择动作最大的 Q 值往往会导致目标值要高于真实值），但是很 容易过犹不及，导致过度估计(Over Estimation)（最终我们得到的 算法模型有很大的偏差(bias)）。为了解决这个问题， DDQN 通 过解耦目标 Q 值动作的选择和目标 Q 值的计算这两步，来达到 消除过度估计的问题。
  
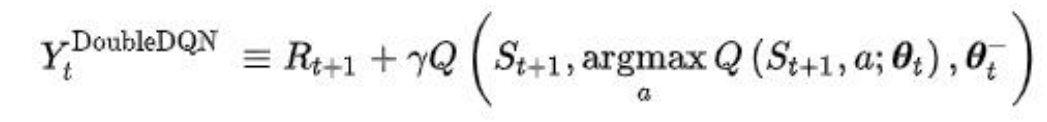
• 算法思想
  
  
  

Prioritized Replay DQN

• 概述
  （1）之前介绍的各种 DQN 都是通过经验回放来采样，在采样的 时候，我们是一视同仁，在经验回放池里面的所有的样本都有相同的被采样到的概率，而这种方式看上去并不高效，对于智能体而言，这些数据的重要程度并不一样，因此提出优先回放（Prioritized Replay）的方法。优先回放的基本思想就是打破均匀 采样，赋予学习效率高的样本以更大的采样权重。
  （2）一个理想的标准是智能体学习的效率越高，权重越大。符合 该标准的一个选择是 TD 偏差δ。TD 偏差越大，说明该状态处 的值函数与 TD 目标的差距越大，智能体的更新量越大，因此该处的学习效率越高。
• 算法思想
  由于引入了经验回放的优先级，那么 Prioritized Replay DQN 的经验回放池和之前的其他 DQN 算法的经验回放池就不一样 了。因为这个优先级大小会影响它被采样的概率。在实际使用中， 我们通常使用 SumTree 这样的二叉树结构来做我们的带优先级 的经验回放池样本的存储。
  
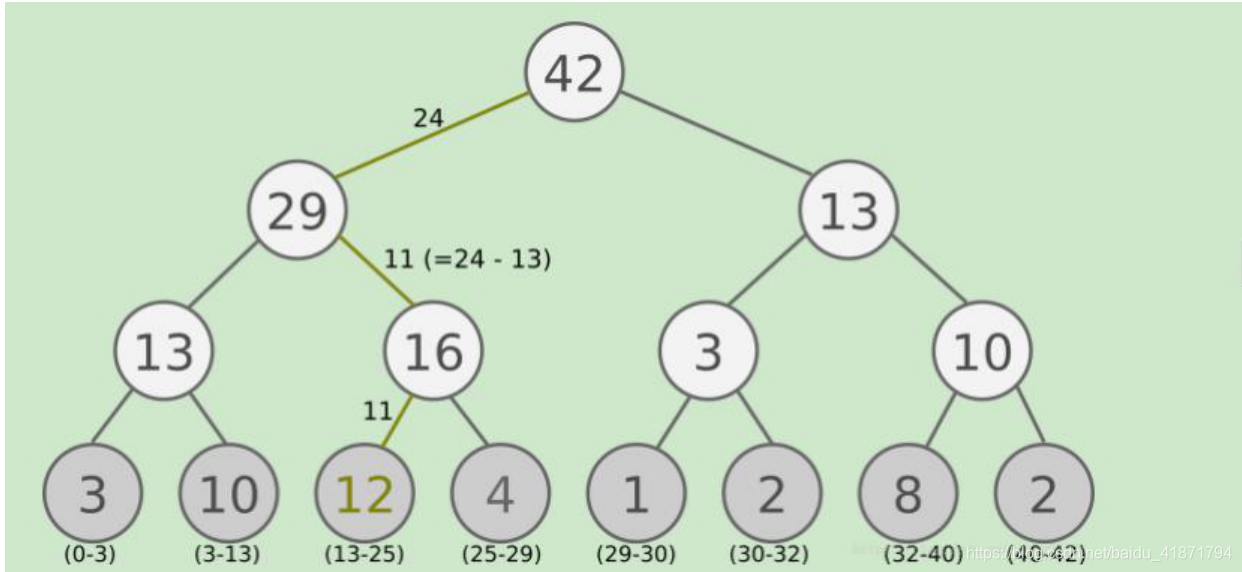
  所有的经验回放样本只保存在最下面的叶子节点上面，一个 节点一个样本。内部节点不保存样本数据。而叶子节点除了保存 数据以外，还要保存该样本的优先级，就是图中的显示的数字。对于内部节点每个节点只保存自己的儿子节点的优先级值之和， 如图中内部节点上显示的数字。
• 算法流程

• 优先回放 DQN 主要有三点改变：
  

参考资料：https://www.cnblogs.com/pinard/p/9797695.html

Dueling DQN

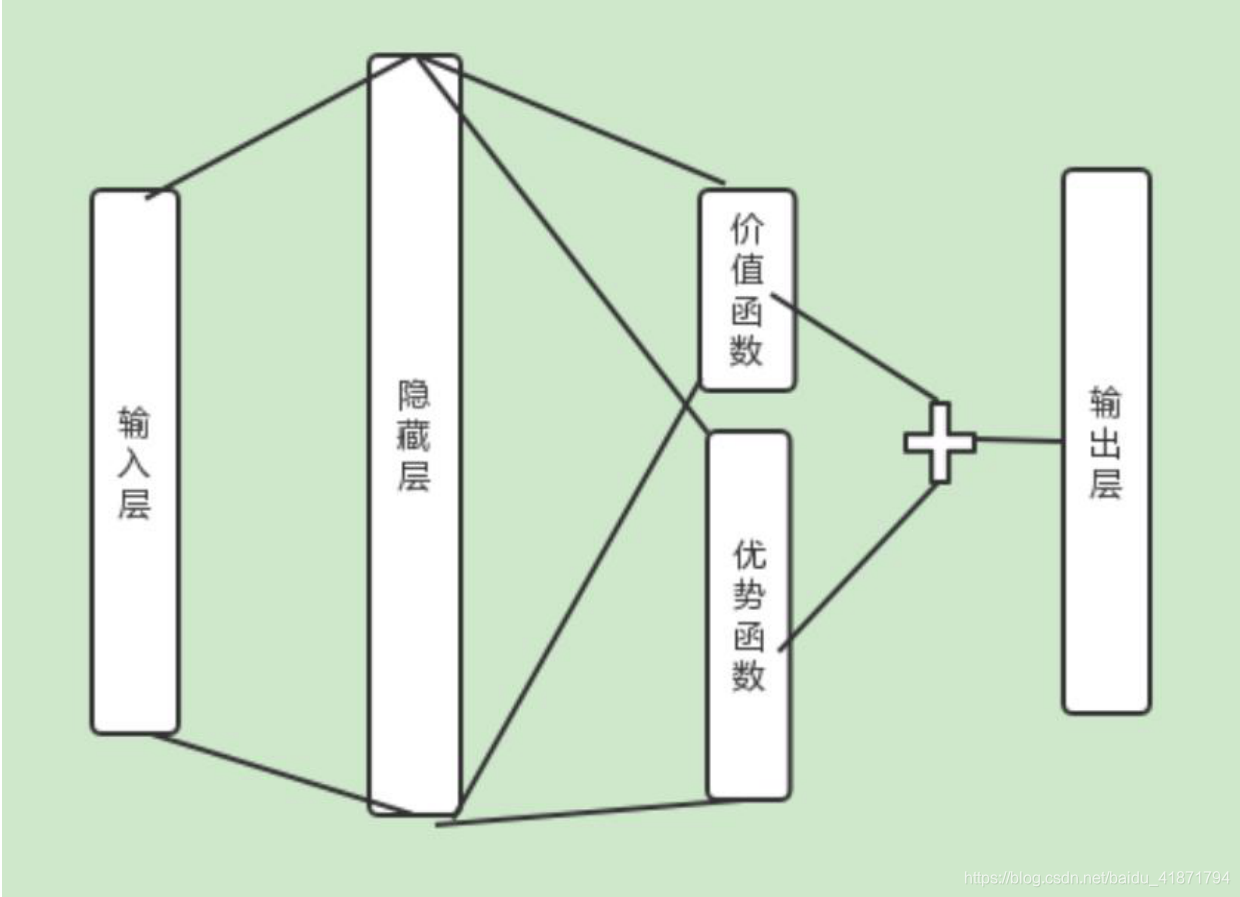
（1）在 Dueling DQN 中，尝试通过优化神经网络的结构来优化算 法，Dueling DQN 将整个模型结构分成了两个部分，一个为状态 值函数，一个为优势函数，即：

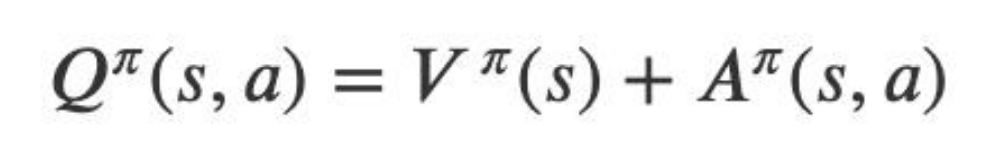
在这里状态值函数和动作无关，而且其也只会返回一个状态值， 优势函数和动作和状态都有关。将上面的表达式细化，则有：

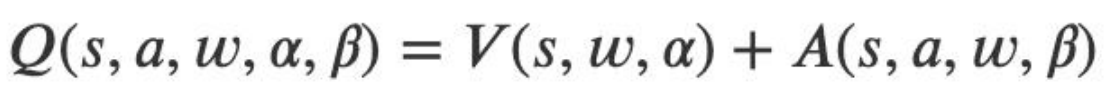
即状态值函数和优势函数会共享一部分参数 w，又各自有自己独 有的参数α和β。

（2）Dueling DQN 原则上可以和上面任意一个 DQN 算法结合，只 需要将 Dueling DQN 的模型结构去替换上面任意一个 DQN 网络 的模型结构。
（3）但一般在使用中我们会对优势函数 A 做中心化处理：

参考资料：https://www.cnblogs.com/pinard/p/9923859.html

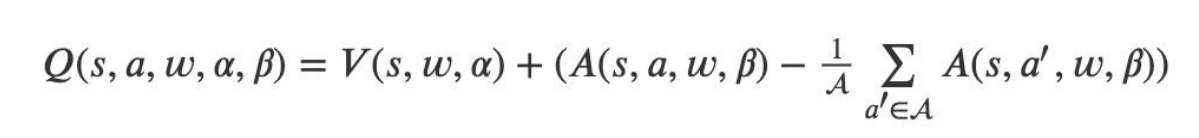
Policy Gradient

• 概述
  （1）基于值的强化学习算法（Value based）的基本思想是根据当 前的状态，计算采取每个动作的价值，然后根据价值贪心的选择 动作。但是 Value based 方法有许多的不足：
  ①不能处理连续动作（如果汽车的速度）
  ②对受限状态下的问题处理能力不足（使用特征来描述状态 空间中的某一个状态时，有可能因为个体观测的限制或者建模的 局限，导致真实环境下本来不同的两个状态却再我们建模后拥有 相同的特征描述）
  （2）如果我们省略中间的步骤，即直接根据当前的状态来选择动 作，就引出了强化学习中另一种重要的算法——Policy Gradient。
  （3）Policy Gradient 的基本思想就是借助神经网络，直接根据状 态 state 输出动作 action 或者动作的概率。‘
• 算法思想
  
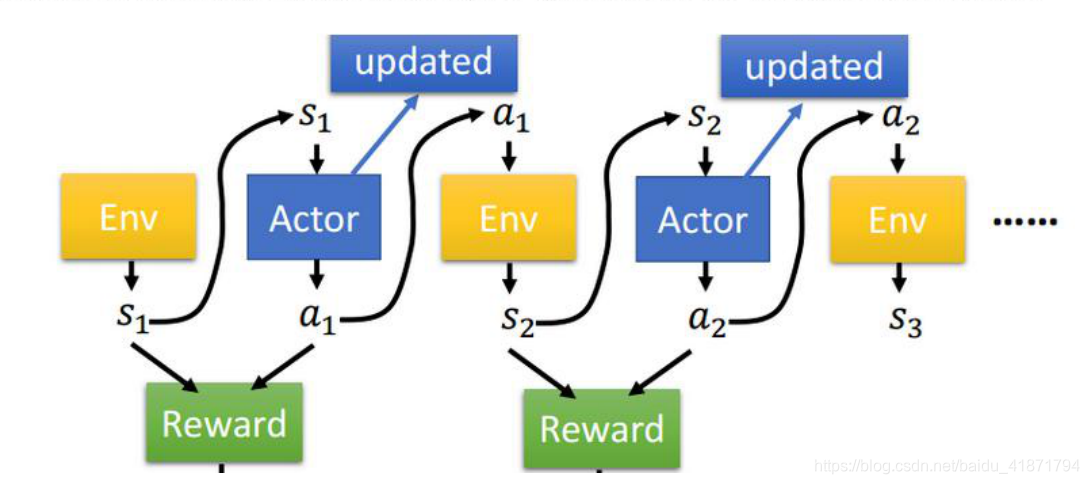
  （1）Policy Gradient 不通过误差反向传播，它通过观测信息选出 一个行为直接进行反向传播，如果一个动作得到的 reward 多，那 么我们就使其出现的概率增加，如果一个动作得到的 reward 少， 我们就使其出现的概率减小。这样好的行为会被增加下一次被选 中的概率，不好的行为会被减弱下次被选中的概率。
  （2）我们需要定义一个策略梯度的优化目标，然后进行梯度上 升，不断的寻找目标函数的最大值（奖励的最大值），找到最优 的梯度。我们可以定义目标函数如下：
  

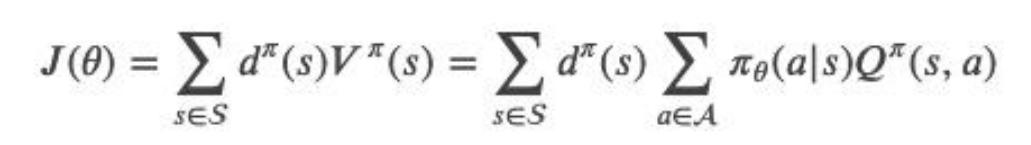
• 蒙特卡洛策略梯度（用来替代值函数的估计）
  

参考博客： https://zhuanlan.zhihu.com/p/107906954 http://fancyerii.github.io/books/rl6/
https://www.cnblogs.com/pinard/p/10137696.html
https://zhuanlan.zhihu.com/p/21725498
https://blog.csdn.net/qq_30615903/article/details/80747380
https://zhuanlan.zhihu.com/p/36494307

Actor-Critic

• 概述
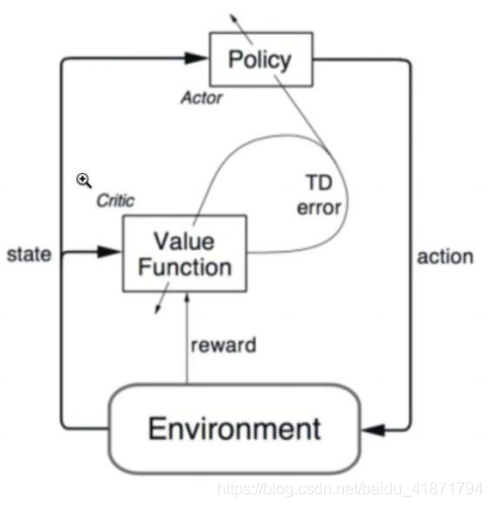
  （1）Actor-Critic 中的 Actor 指的是 Policy Gradient 的策略函数负 责生成动作 Action 和环境交互，而 Critic 则是之前说到的值函数， 负责评估 Action 的表现，给出奖励值，并知道 Action 下一个阶 段的动作。
  （2）所以在 Actor-Critic 中需要给出两组近似，即策略函数的近 似以及价值函数的近似，即：
  
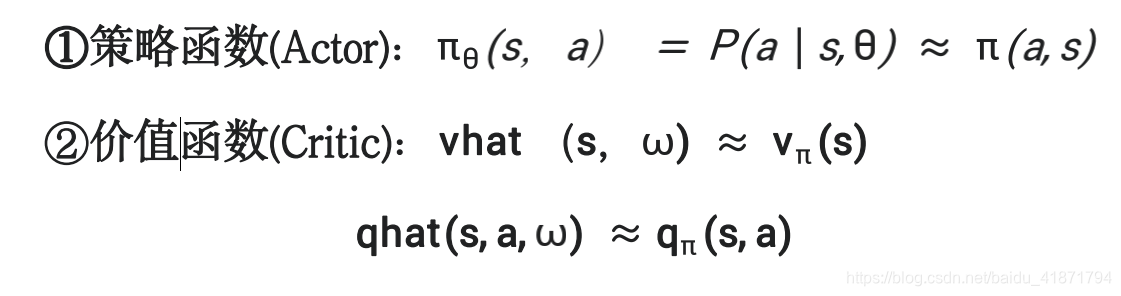
  Critic：更新动作值函数参数 ω；
  Actor：以 Critic 所指导的方向更新策略参数 θ；
  （3）对于 Critic 来说，可以通过一个 Q 网络作为 Critic，这个 Q 网络的输入可以是状态，而输出是每个动作的价值或者最优动作的价值。
  （4）总结：Critic 通过 Q 网络计算状态的最优价值 vt, 而 Actor 利用 vt 这个最优价值迭代更新策略函数的参数θ,进而选择动作，并得到反馈和新的状态，Critic 使用反馈和新的状态更新 Q 网络参数 w, 在后面 Critic 会使用新的网络参数 w 来帮 Actor 计算 状态的最优价值。

• 算法思想
  
  

参考资料：https://www.zhihu.com/question/56692640
https://www.jianshu.com/p/25c09ae3d206
https://zhuanlan.zhihu.com/p/36494307
https://www.cnblogs.com/pinard/p/10272023.html
https://blog.csdn.net/qq_30615903/article/details/80774384

DDPG (Deep Deterministic Policy Gradient)算法

• 概述
  （1）DDPG 也是一种 model free, off-policy 的算法，同样使用了深度神经网络进行值函数的近似。
  （2）但与 DQN 不同的是，DQN 只能解决离散且维度不高的 action spaces 的问题。而 DDPG 可以解决连续动作空间问题（如汽车的 速度），DQN 是 value based 方法，即只有一个值函数网络，而 DDPG 是 actor-critic 方法，即既有值函数网络(critic)，又有策略 网络(actor)
• 算法思想
  （1）强化学习是一个反复迭代的过程，每一次迭代要解决两个问 题：给定一个策略求值函数，和根据值函数来更新策略。
  （2）DDPG 中使用一个神经网络来近似值函数，此值函数网络又 称 critic 网络，它的输入是 action 与 observation [a,s]，输出是 Q(s,a)；另外使用一个神经网络来近似策略函数，此 policy 网络 又称 actor 网络，它的输入是 observation s，输出是 action a.
  
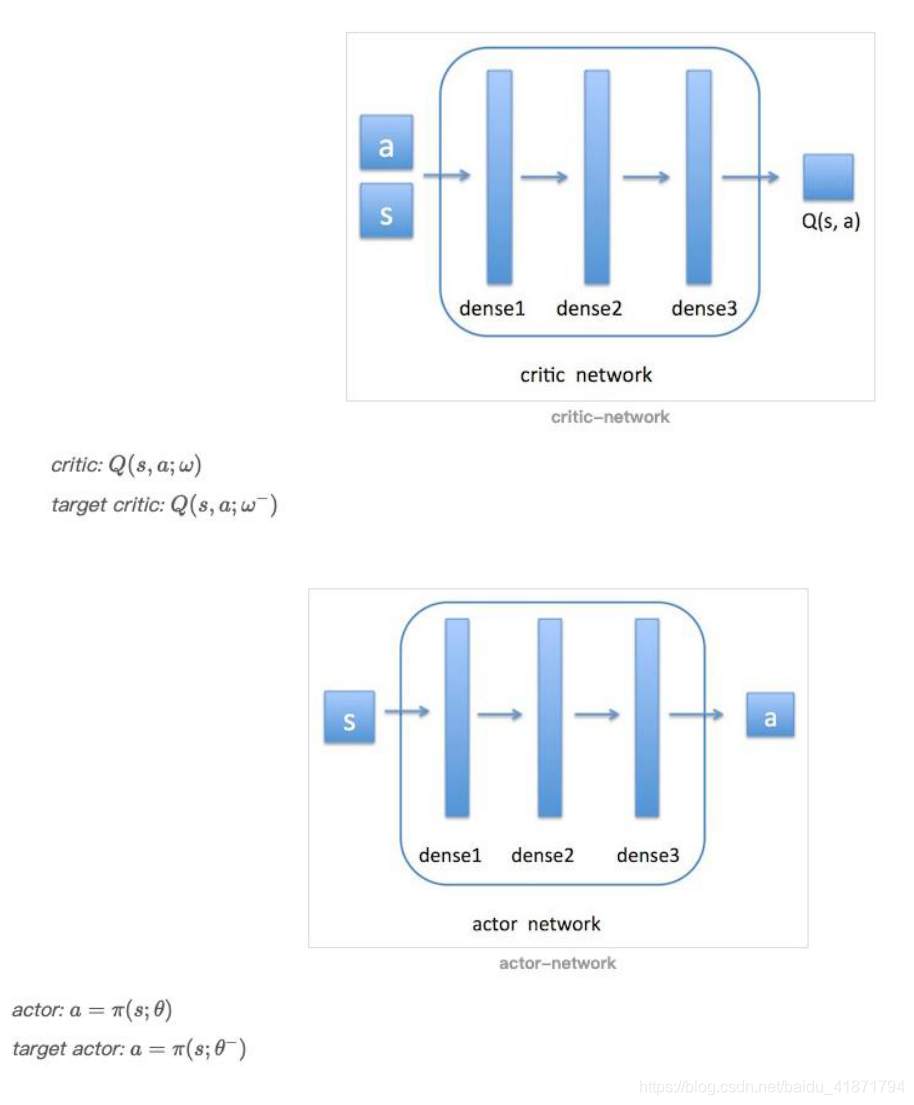
  注：ω−表示它比 Q 网络的权重 ω更新得要慢一些。
  （3）两个网络之间的联系：首先环境会给出一个 observation，智能体根据 actor 网络（后面会讲到在此网络基础上增加噪声）做 出决策 action，环境收到此 action 后会给出一个奖励 Reward，及新的 observation。这个过程是一个 step。此时我们要根据 Reward 去更新 critic 网络，然后沿 critic 建议的方向去更新 actor 网络。 接着进入下一个 step。如此循环下去，直到我们训练出了一个好 的 actor 网络。
  （4）与 DQN 一样，DDPG 中也使用了 target 网络来保证参数的收 敛。假设 critic 网络为 Q(s,a;ω)， 它对应的 target critic 网络为 Q(s,a;ω−)。actor 网络为π(s;θ)，它对应的 target actor 网络为 π(s;θ−)。
  
  

参考博客：https://wanjun0511.github.io/2017/11/19/DDPG/ https://arxiv.org/pdf/1509.02971.pdf

• 算法流程
  DDGP与DQN类似，也使用了深度神经网络进行值函数的近似，经验回放和 target 网络，而DDPG 每一步都会更新 target 网络，只不过更新的幅度非常小。
  

参考资料： https://arxiv.org/pdf/1509.02971.pdf

A3C

• 概述
  （1）Actor-Critic 算法很难收敛，所以针对 Actor-Critic 有很多优 化版的算法，A3C 就是一种优化比较好的算法。
  （2）之前的 DQN 算法，为了方便收敛使用了经验回放的技巧。 A3C 更进一步，克服了一些经验回放的问题（回放池经验数据相 关性太强，用于训练的时候效果很可能不佳）。
  （3） A3C 利用多线程的方法，同时在多个线程里面分别和环境进 行交互学习，每个线程都把学习的成果汇总起来，整理保存在一个公共的地方。并且，定期从公共的地方把大家的齐心学习的成 果拿回来，指导自己和环境后面的学习交互。
  （4）通过这种方法，A3C 避免了经验回放相关性过强的问题，同时做 到了异步并发的学习模型。
• 算法优化
  （1）异步训练框架：
  使用一个 Global Network，一个公共的神经网络模型，这个 神经网络包括 Actor 网络和 Critic 网络两部分的功能。下面有 n 个 worker 线程，每个线程里有和公共的神经网络一样的网络结 构，每个线程会独立的和环境进行交互得到经验数据，这些线程 之间互不干扰，独立运行。每个线程和环境交互到一定量的数据 后，就计算在自己线程里的神经网络损失函数的梯度，但是这些 梯度却并不更新自己线程里的神经网络，而是去更新公共的神经 网络。也就是 n 个线程会独立的使用累积的梯度分别更新公共部 分的神经网络模型参数。每隔一段时间，线程会将自己的神经网 络的参数更新为公共神经网络的参数，进而指导后面的环境交 互。
  （2）网络结构优化
  
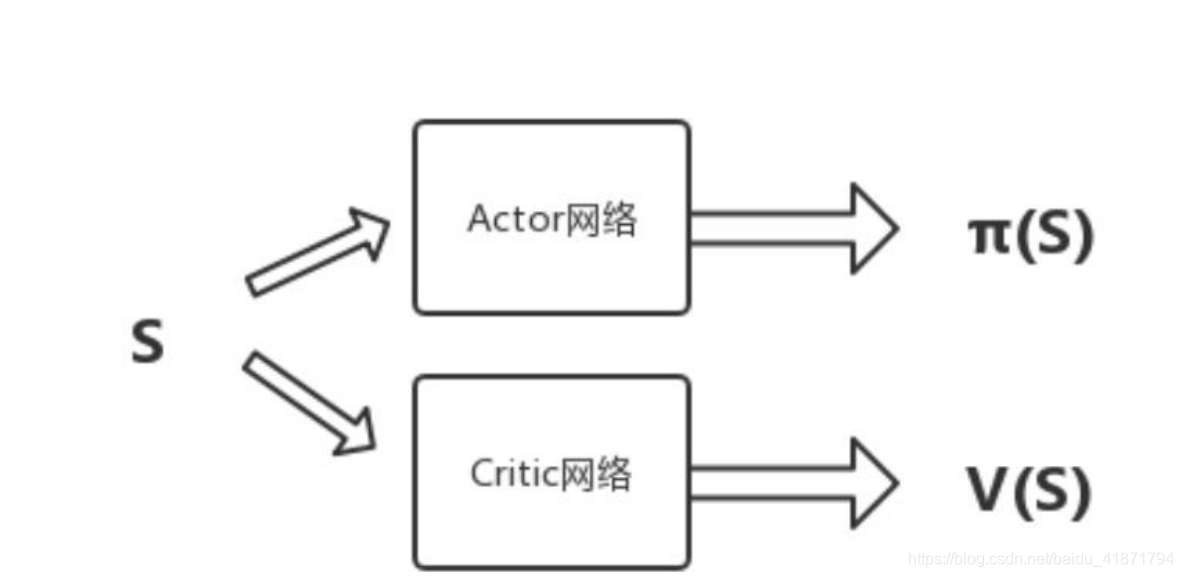
  Actor-Critic 中，使用了两个不同的网络 Actor 和 Critic。在 A3C 这里，我们把两个网络放到了一起，即输入状态 S,可以同时输出 状态价值 V,和对应的策略π。
  （3）Critic 评估点的优化
  在 A3C 中，采样更进一步，使用了 N 步采样，以加速收敛。
• 算法思想
  A3C 的基本思想，其实就是 Actor-Critic 的基本思想，对输 出的动作进行好坏评估，如果动作被认为是好的，那么就调整行 动网络（Actor Network）使该动作出现的可能性增加。反之如果 动作被认为是坏的，则使该动作出现的可能性减少。通过反复的 训练，不断调整行动网络找到最优的动作。
  
  原文的算法步骤：
  

参考资料：https://zhuanlan.zhihu.com/p/32596470
https://www.cnblogs.com/pinard/p/10334127.html

强化学习的应用

产品级应用（在实际系统中的应用）

• （1）自动机器学习 AutoML 将机器学习应用于现实问题的 end-to-end 流程自动化的过程https://blog.csdn.net/guanxs/article/details/101400992
• （2）决策服务 Decision Service 金融决策自动化，为企业制定长期的战略目标
  https://aws.amazon.com/cn/blogs/china/automated-decision-making-
  with-deep-reinforcement-learning/
• （3）推荐系统 https://zhuanlan.zhihu.com/p/82717109
• （4）广告投放
• （5）智能交通：交通灯控制（通过控制交通灯来解决拥堵问题）

机器人

强化学习的传统应用方向，比如谷歌的 AlphaGo。

计算机视觉

（1）识别
（2）情景理解
（3）交互感知

计算机系统

https://easyai.tech/blog/applications-of-reinforcement-learning-in-r eal-world/
（1）计算机集群中的资源管理 将有限的资源分配给不同的任务，如何使用 RL 自动学习分 配和安排计算机资源到等待工作，目的是最小化平均工作减速。
（2）软件测试
（3）系统安全

科学、工程和艺术

游戏

强化学习的很多成果都被做成了游戏

自然语言处理

参考资料：https://zhuanlan.zhihu.com/p/78191585
（这篇博客中给 出了许多强化学习应用于实际的论文）