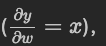介绍Pytorch中的自动微分系统（Autograd）
用Tensor训练网络很方便，但从上一小节最后的线性回归例子来看，反向传播过程需要手动实现。这对于像线性回归等较为简单的模型来说，还可以应付，但实际使用中经常出现非常复杂的网络结构，此时如果手动实现反向传播，不仅费时费力，而且容易出错，难以检查。torch.autograd就是为方便用户使用，而专门开发的一套自动求导引擎，它能够根据输入和前向传播过程自动构建计算图，并执行反向传播。

计算图(Computation Graph)是现代深度学习框架如PyTorch和TensorFlow等的核心，其为高效自动求导算法——反向传播(Back Propogation)提供了理论支持，了解计算图在实际写程序过程中会有极大的帮助。本节将涉及一些基础的计算图知识，但并不要求读者事先对此有深入的了解。

Variable

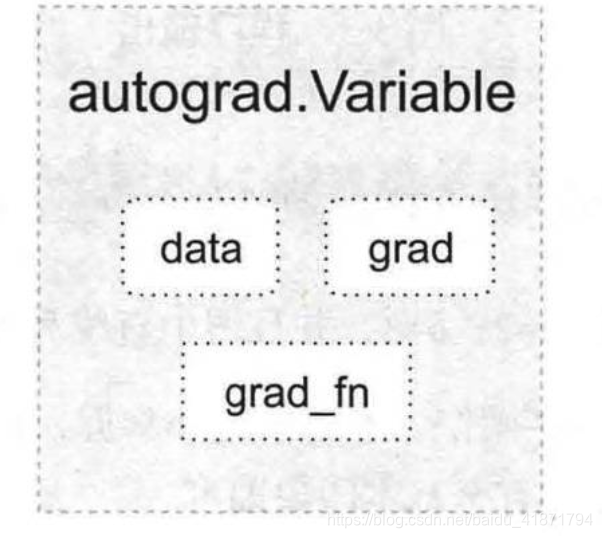
PyTorch在autograd模块中实现了计算图的相关功能，autograd中的核心数据结构是Variable。Variable封装了tensor，并记录对tensor的操作记录用来构建计算图。Variable的数据结构如图所示，主要包含三个属性：
在这里插入图片描述

data：保存variable所包含的tensor
grad：保存data对应的梯度，grad也是variable，而不是tensor，它与data形状一致。
grad_fn：指向一个Function，记录tensor的操作历史，即它是什么操作的输出，用来构建计算图。如果某一个变量是由用户创建，则它为叶子节点，对应的grad_fn等于None。

Variable的构造函数需要传入tensor，同时有两个可选参数：

requires_grad (bool)：是否需要对该variable进行求导
volatile (bool)：意为”挥发“，设置为True，则构建在该variable之上的图都不会求导，专为推理阶段设计

Variable提供了大部分tensor支持的函数，但其不支持部分inplace函数，因这些函数会修改tensor自身，而在反向传播中，variable需要缓存原来的tensor来计算反向传播梯度。如果想要计算各个Variable的梯度，只需调用根节点variable的backward方法，autograd会自动沿着计算图反向传播，计算每一个叶子节点的梯度。

variable.backward(grad_variables=None, retain_graph=None, create_graph=None)主要有如下参数：

grad_variables：形状与variable一致，对于y.backward()，grad_variables相当于链式法则 ${dz \over dx}={dz \over dy} \times {dy \over dx}$ 中的 $\textbf {dz} \over \textbf {dy}$ 。grad_variables也可以是tensor或序列。
retain_graph：反向传播需要缓存一些中间结果，反向传播之后，这些缓存就被清空，可通过指定这个参数不清空缓存，用来多次反向传播。
create_graph：对反向传播过程再次构建计算图，可通过backward of backward实现求高阶导数。

from __future__ import print_function
import torch 
from torch.autograd import Variable

# 从tensor中创建variable，指定需要求导
a = Variable(torch.ones(3,4), requires_grad = True) 

#b不需要求导
b =  Variable(torch.zeros(3,4))

# 函数的使用与tensor一致
# 也可写成c = a + b
c = a.add(b)

d = c.sum()
d.backward() # 反向传播

# 注意二者的区别
# 前者在取data后变为tensor，而后从tensor计算sum得到float
# 后者计算sum后仍然是Variable
c.data.sum(), c.sum()
#(tensor(12.), tensor(12., grad_fn=<SumBackward0>))

# 此处虽然没有指定c需要求导，但c依赖于a，而a需要求导，
# 因此c的requires_grad属性会自动设为True
a.requires_grad, b.requires_grad, c.requires_grad
#(True, False, True)

# 由用户创建的variable属于叶子节点，对应的grad_fn是None
a.is_leaf, b.is_leaf, c.is_leaf
#(True, True, False)

# c.grad是None, 因c不是叶子节点，它的梯度是用来计算a的梯度
# 所以虽然c.requires_grad = True,但其梯度计算完之后即被释放
c.grad is None
#True

计算下面这个函数的导函数：

$y = x^2\bullet e^x$

它的导函数是：

${dy \over dx} = 2x\bullet e^x + x^2 \bullet e^x$

来看看autograd的计算结果与手动求导计算结果的误差。

def f(x):
    '''计算y'''
    y = x**2 * t.exp(x)
    return y

def gradf(x):
    '''手动求导函数'''
    dx = 2*x*t.exp(x) + x**2*t.exp(x)
    return dx

#手动计算导数
x = Variable(torch.randn(3,4), requires_grad = True)
y = f(x)

#自动计算
y.backward(torch.ones(y.size())) # grad_variables形状与y一致
x.grad
# autograd的计算结果与利用公式手动计算的结果一致
gradf(x)

计算图

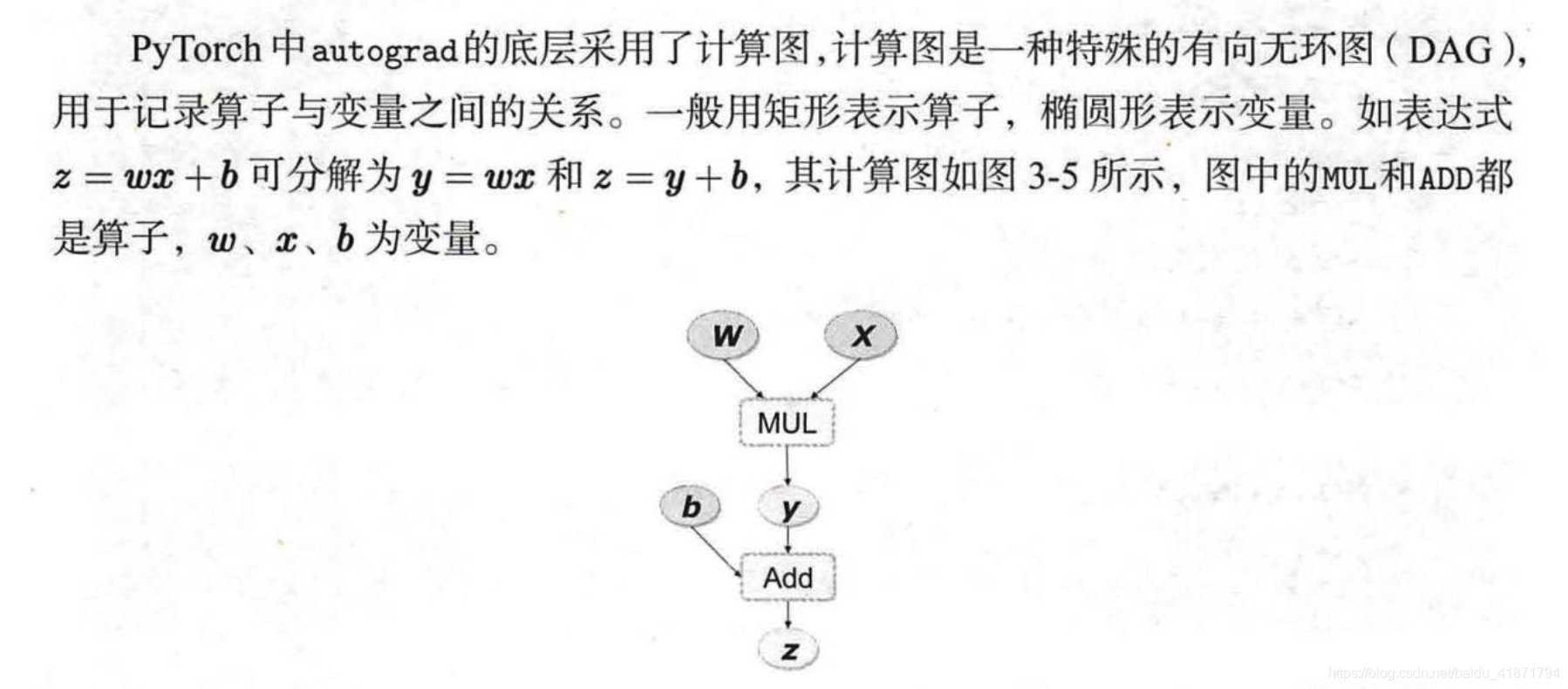
在这里插入图片描述

在PyTorch实现中，autograd会随着用户的操作，记录生成当前variable的所有操作，并由此建立一个有向无环图。用户每进行一个操作，相应的计算图就会发生改变。更底层的实现中，图中记录了操作Function，每一个变量在图中的位置可通过其grad_fn属性在图中的位置推测得到。在反向传播过程中，autograd沿着这个图从当前变量（根节点 $\textbf{z}$ ）溯源，可以利用链式求导法则计算所有叶子节点的梯度。每一个前向传播操作的函数都有与之对应的反向传播函数用来计算输入的各个variable的梯度，这些函数的函数名通常以Backward结尾。下面结合代码学习autograd的实现细节。

x = Variable(torch.ones(1))
b = Variable(torch.rand(1), requires_grad = True)
w = Variable(torch.rand(1), requires_grad = True)
y = w * x # 等价于y=w.mul(x)
z = y + b # 等价于z=y.add(b)

x.requires_grad, b.requires_grad, w.requires_grad
#(False, True, True)

# 虽然未指定y.requires_grad为True，但由于y依赖于需要求导的w
# 故而y.requires_grad为True
y.requires_grad
#True

# grad_fn可以查看这个variable的反向传播函数，
# z是add函数的输出，所以它的反向传播函数是AddBackward
z.grad_fn 
#<AddBackward0 at 0x7f8761eebb20>

# next_functions保存grad_fn的输入，是一个tuple，tuple的元素也是Function
# 第一个是y，它是乘法(mul)的输出，所以对应的反向传播函数y.grad_fn是MulBackward
# 第二个是b，它是叶子节点，由用户创建，grad_fn为None，但是有
z.grad_fn.next_functions 
#((<MulBackward0 at 0x7f8761eebb80>, 0),
#(<AccumulateGrad at 0x7f87911e6970>, 0))

# 第一个是w，叶子节点，需要求导，梯度是累加的
# 第二个是x，叶子节点，不需要求导，所以为None
y.grad_fn.next_functions
#((<AccumulateGrad at 0x7f87911e6100>, 0), (None, 0))

# 叶子节点的grad_fn是None
w.grad_fn,x.grad_fn
#(None, None)

计算w的梯度的时候，需要用到x的数值
在这里插入图片描述
，这些数值在前向过程中会保存成buffer，在计算完梯度之后会自动清空。为了能够多次反向传播需要指定retain_graph来保留这些buffer。

# 使用retain_graph来保存buffer
z.backward(retain_graph=True)
w.grad

变量的requires_grad属性默认为False，如果某一个节点requires_grad被设置为True，那么所有依赖它的节点requires_grad都是True。volatile=True是另外一个很重要的标识，它能够将所有依赖于它的节点全部都设为volatile=True，其优先级比requires_grad=True高。volatile=True的节点不会求导，即使requires_grad=True，也无法进行反向传播。对于不需要反向传播的情景（如inference，即测试推理时），该参数可实现一定程度的速度提升，并节省约一半显存，因其不需要分配空间计算梯度。

x = Variable(torch.ones(1))
w = Variable(torch.rand(1), requires_grad=True)
y = x * w
# y依赖于w，而w.requires_grad = True
x.requires_grad, w.requires_grad, y.requires_grad
#(False, True, True)

在反向传播过程中非叶子节点的导数计算完之后即被清空。若想查看这些变量的梯度，有两种方法：

使用autograd.grad函数
使用hook

x =  Variable(torch.ones(3), requires_grad=True)
w =  Variable(torch.rand(3), requires_grad=True)
y = x * w
# y依赖于w，而w.requires_grad = True
z = y.sum()
x.requires_grad, w.requires_grad, y.requires_grad
#(True, True, True)


# 非叶子节点grad计算完之后自动清空，y.grad是None
z.backward()
(x.grad, w.grad, y.grad)


# 第一种方法：使用grad获取中间变量的梯度
x =  Variable(torch.ones(3), requires_grad=True)
w =  Variable(torch.rand(3), requires_grad=True)
y = x * w
z = y.sum()
# z对y的梯度，隐式调用backward()
torch.autograd.grad(z, y)


# 第二种方法：使用hook
# hook是一个函数，输入是梯度，不应该有返回值
def variable_hook(grad):
    print('y的梯度： \r\n',grad)

x = Variable(torch.ones(3), requires_grad=True)
w =  Variable(torch.rand(3), requires_grad=True)
y = x * w
# 注册hook
hook_handle = y.register_hook(variable_hook)
z = y.sum()
z.backward()

# 除非你每次都要用hook，否则用完之后记得移除hook
hook_handle.remove()

在PyTorch中计算图的特点可总结如下：

autograd根据用户对variable的操作构建其计算图。对变量的操作抽象为Function。
对于那些不是任何函数(Function)的输出，由用户创建的节点称为叶子节点，叶子节点的grad_fn为None。叶子节点中需要求导的variable，具有AccumulateGrad标识，因其梯度是累加的。
variable默认是不需要求导的，即requires_grad属性默认为False，如果某一个节点requires_grad被设置为True，那么所有依赖它的节点requires_grad都为True。
variable的volatile属性默认为False，如果某一个variable的volatile属性被设为True，那么所有依赖它的节点volatile属性都为True。volatile属性为True的节点不会求导，volatile的优先级比requires_grad高。
多次反向传播时，梯度是累加的。反向传播的中间缓存会被清空，为进行多次反向传播需指定retain_graph=True来保存这些缓存。
非叶子节点的梯度计算完之后即被清空，可以使用autograd.grad或hook技术获取非叶子节点的值。
variable的grad与data形状一致，应避免直接修改variable.data，因为对data的直接操作无法利用autograd进行反向传播
反向传播函数backward的参数grad_variables可以看成链式求导的中间结果，如果是标量，可以省略，默认为1
PyTorch采用动态图设计，可以很方便地查看中间层的输出，动态的设计计算图结构。

用Variable实现线性回归


import torch as t
from torch.autograd import Variable as V
%matplotlib inline
from matplotlib import pyplot as plt
from IPython import display

# 设置随机数种子，为了在不同人电脑上运行时下面的输出一致
t.manual_seed(1000) 

def get_fake_data(batch_size=8):
    ''' 产生随机数据：y = x*2 + 3，加上了一些噪声'''
    x = t.rand(batch_size,1) * 20
    y = x * 2 + (1 + t.randn(batch_size, 1))*3
    return x, y

# 来看看产生x-y分布是什么样的
x, y = get_fake_data()
plt.scatter(x.squeeze().numpy(), y.squeeze().numpy())


# 随机初始化参数
w = V(t.rand(1,1), requires_grad=True)
b = V(t.zeros(1,1), requires_grad=True)

lr =0.001 # 学习率

for ii in range(8000):
    x, y = get_fake_data()
    x, y = V(x.float()), V(y.float())
    
    # forward：计算loss
    y_pred = x.mm(w) + b.expand_as(y)
    loss = 0.5 * (y_pred - y) ** 2
    loss = loss.sum()
    
    # backward：手动计算梯度
    loss.backward()
    
    # 更新参数
    w.data.sub_(lr * w.grad.data)
    b.data.sub_(lr * b.grad.data)
    
    # 梯度清零
    w.grad.data.zero_()
    b.grad.data.zero_()
    
    if ii%1000 ==0:
        # 画图
        display.clear_output(wait=True)
        x = t.arange(0, 20).view(-1, 1).float()
        y = x.mm(w.data) + b.data.expand_as(x)
        plt.plot(x.numpy(), y.numpy()) # predicted
        
        x2, y2 = get_fake_data(batch_size=20) 
        plt.scatter(x2.numpy(), y2.numpy()) # true data
        
        plt.xlim(0,20)
        plt.ylim(0,41)   
        plt.show()
        plt.pause(0.5)
        
print(w.data.squeeze()[0], b.data.squeeze()[0])