介绍Pytorch中的张量系统(Tensor)
Tensor
from __future__ import print_function
import torch as t
t.__version__
|
基础操作
从接口的角度来讲,对tensor的操作可分为两类:
torch.function,如torch.save等。- 另一类是
tensor.function,如tensor.view等。
为方便使用,对tensor的大部分操作同时支持这两类接口,在本书中不做具体区分,如torch.sum (torch.sum(a, b))与tensor.sum (a.sum(b))功能等价。
而从存储的角度来讲,对tensor的操作又可分为两类:
- 不会修改自身的数据,如
a.add(b), 加法的结果会返回一个新的tensor。
- 会修改自身的数据,如
a.add_(b), 加法的结果仍存储在a中,a被修改了。
函数名以_结尾的都是inplace方式, 即会修改调用者自己的数据,在实际应用中需加以区分。
| 函数 |
功能 |
| Tensor(*sizes) |
基础构造函数 |
| ones(*sizes) |
全1Tensor |
| zeros(*sizes) |
全0Tensor |
| eye(*sizes) |
对角线为1,其他为0 |
| arange(s,e,step |
从s到e,步长为step |
| linspace(s,e,steps) |
从s到e,均匀切分成steps份 |
| rand/randn(*sizes) |
均匀/标准分布 |
| normal(mean,std)/uniform(from,to) |
正态分布/均匀分布 |
| randperm(m) |
随机排列 |
其中使用Tensor函数新建tensor是最复杂多变的方式,它既可以接收一个list,并根据list的数据新建tensor,也能根据指定的形状新建tensor,还能传入其他的tensor,下面举几个例子。
a = t.Tensor(2, 3)
b = t.Tensor([[1,2,3],[4,5,6]])
b.tolist()
|
- tensor.size()返回torch.Size对象,它是tuple的子类,但其使用方式与tuple略有区别
b_size = b.size()
b.numel()
c = t.Tensor(b_size)
d = t.Tensor((2, 3))
|
- 除了
tensor.size(),还可以利用tensor.shape直接查看tensor的形状,tensor.shape等价于tensor.size()
- 需要注意的是,
t.Tensor(*sizes)创建tensor时,系统不会马上分配空间,只是会计算剩余的内存是否足够使用,使用到tensor时才会分配,而其它操作都是在创建完tensor之后马上进行空间分配。其它常用的创建tensor的方法举例如下。
t.ones(2, 3)
t.zeros(2, 3)
t.arange(1, 6, 2)
t.linspace(1, 10, 3)
t.randn(2, 3)
t.randperm(5)
t.eye(2, 3)
|
常用Tensor操作
- 通过
tensor.view方法可以调整tensor的形状,但必须保证调整前后元素总数一致。view不会修改自身的数据,返回的新tensor与源tensor共享内存,也即更改其中的一个,另外一个也会跟着改变。在实际应用中可能经常需要添加或减少某一维度,这时候squeeze和unsqueeze两个函数就派上用场了。
a = t.arange(0, 6)
a.view(2, 3)
b = a.view(-1, 3)
b.unsqueeze(1)
b.unsqueeze(-2)
c = b.view(1, 1, 1, 2, 3)
c.squeeze(0)
c.squeeze()
a[1] = 100
b
|
resize是另一种可用来调整size的方法,但与view不同,它可以修改tensor的大小。如果新大小超过了原大小,会自动分配新的内存空间,而如果新大小小于原大小,则之前的数据依旧会被保存,看一个例子。
b.resize_(1, 3)
b.resize_(3, 3)
|
索引操作
- Tensor支持与numpy.ndarray类似的索引操作,语法上也类似,下面通过一些例子,讲解常用的索引操作。如无特殊说明,索引出来的结果与原tensor共享内存,也即修改一个,另一个会跟着修改。
a = t.randn(3, 4)
a[0]
a[:, 0]
a[0][2]
a[0, -1]
a[:2]
print(a[0:1, :2])
print(a[0, :2])
a > 1
a[a>1]
a[t.LongTensor([0,1])]
|
| 函数 |
功能 |
| index_select(input, dim, index) |
在指定维度dim上选取,比如选取某些行、某些列 |
| masked_select(input, mask) |
例子如上,a[a>0],使用ByteTensor进行选取 |
| non_zero(input) |
非0元素的下标 |
| gather(input, dim, index) |
根据index,在dim维度上选取数据,输出的size与index一样 |
gather是一个比较复杂的操作,对一个2维tensor,输出的每个元素如下:
out[i][j] = input[index[i][j]][j]
out[i][j] = input[i][index[i][j]]
|
a = t.arange(0, 16).view(4, 4)
index = t.LongTensor([[0,1,2,3]])
a.gather(0, index)
output:
tensor([[ 0, 5, 10, 15]])
index = t.LongTensor([[3,2,1,0]]).t()
a.gather(1, index)
output:
tensor([[ 3],
[ 6],
[ 9],
[12]])
index = t.LongTensor([[3,2,1,0]])
a.gather(0, index)
output:
tensor([[12, 9, 6, 3]])
index = t.LongTensor([[0,1,2,3],[3,2,1,0]]).t()
b = a.gather(1, index)
output:
tensor([[ 0, 3],
[ 5, 6],
[10, 9],
[15, 12]])
|
- 与
gather相对应的逆操作是scatter_,gather把数据从input中按index取出,而scatter_是把取出的数据再放回去。注意scatter_函数是inplace操作。
out = input.gather(dim, index)
-->近似逆操作
out = Tensor()
out.scatter_(dim, index)
|
c = t.zeros(4,4)
c.scatter_(1, index, b)
|
高级索引
Pytorch目前已经支持绝大多数numpy的高级索引
x = t.arange(0,27).view(3,3,3)
output:
tensor([[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8]],
[[ 9, 10, 11],
[12, 13, 14],
[15, 16, 17]],
[[18, 19, 20],
[21, 22, 23],
[24, 25, 26]]])
x[[1, 2], [1, 2], [2, 0]]
output:
tensor([14, 24])
x[[2, 1, 0], [0], [1]]
output:
tensor([19, 10, 1])
x[[0, 2], ...]
output:
tensor([[[ 0, 1, 2],
[ 3, 4, 5],
[ 6, 7, 8]],
[[18, 19, 20],
[21, 22, 23],
[24, 25, 26]]])
rows = np.array([[0,0],[3,3]])
cols = np.array([[0,2],[0,2]])
y = x[rows,cols]
print (y)
|
Tensor类型
Tensor有不同的数据类型,如表示,每种类型分别对应有CPU和GPU版本(HalfTensor除外)。默认的tensor是FloatTensor,可通过t.set_default_tensor_type 来修改默认tensor类型(如果默认类型为GPU tensor,则所有操作都将在GPU上进行)。Tensor的类型对分析内存占用很有帮助。例如对于一个size为(1000, 1000, 1000)的FloatTensor,它有1000*1000*1000=10^9个元素,每个元素占32bit/8 = 4Byte内存,所以共占大约4GB内存/显存。HalfTensor是专门为GPU版本设计的,同样的元素个数,显存占用只有FloatTensor的一半,所以可以极大缓解GPU显存不足的问题,但由于HalfTensor所能表示的数值大小和精度有限[^2],所以可能出现溢出等问题。
| 数据类型 |
CPU tensor |
GPU tensor |
| 32-bit 浮点 |
torch.FloatTensor |
torch.cuda.FloatTensor |
| 64-bit 浮点 |
torch.DoubleTensor |
torch.cuda.DoubleTensor |
| 16-bit 半精度浮点 |
N/A |
torch.cuda.HalfTensor |
| 8-bit 无符号整形(0~255) |
torch.ByteTensor |
torch.cuda.ByteTensor |
| 8-bit 有符号整形(-128~127) |
torch.CharTensor |
torch.cuda.CharTensor |
| 16-bit 有符号整形 |
torch.ShortTensor |
torch.cuda.ShortTensor |
| 32-bit 有符号整形 |
torch.IntTensor |
torch.cuda.IntTensor |
| 64-bit 有符号整形 |
torch.LongTensor |
torch.cuda.LongTensor |
各数据类型之间可以互相转换,type(new_type)是通用的做法,同时还有float、long、half等快捷方法。CPU tensor与GPU tensor之间的互相转换通过tensor.cuda和tensor.cpu方法实现。Tensor还有一个new方法,用法与t.Tensor一样,会调用该tensor对应类型的构造函数,生成与当前tensor类型一致的tensor。
t.set_default_tensor_type('torch.IntTensor')
a = t.Tensor(2,3) a
b = a.float()
t.set_default_tensor_type('torch.FloatTensor')
|
逐元素操作
这部分操作会对tensor的每一个元素(point-wise,又名element-wise)进行操作,此类操作的输入与输出形状一致。常用的操作如表所示。
| 函数 |
功能 |
| abs/sqrt/div/exp/fmod/log/pow… |
绝对值/平方根/除法/指数/求余/求幂… |
| cos/sin/asin/atan2/cosh… |
相关三角函数 |
| ceil/round/floor/trunc |
上取整/四舍五入/下取整/只保留整数部分 |
| clamp(input, min, max) |
超过min和max部分截断 |
| sigmod/tanh… |
激活函数 |
对于很多操作,例如div、mul、pow、fmod等,PyTorch都实现了运算符重载,所以可以直接使用运算符。如a ** 2 等价于torch.pow(a,2), a * 2等价于torch.mul(a,2)。
其中clamp(x, min, max)的输出满足以下公式:
yi=⎩⎪⎨⎪⎧min,xi,max,if xi<minif min≤xi≤maxif xi>max
clamp常用在某些需要比较大小的地方,如取一个tensor的每个元素与另一个数的较大值。
a = t.arange(0, 6).view(2, 3)
t.cos(a)
a % 3
a ** 2
print(a)
t.clamp(a, min=3)
|
归并操作
此类操作会使输出形状小于输入形状,并可以沿着某一维度进行指定操作。如加法sum,既可以计算整个tensor的和,也可以计算tensor中每一行或每一列的和。常用的归并操作如表所示。
| 函数 |
功能 |
| mean/sum/median/mode |
均值/和/中位数/众数 |
| norm/dist |
范数/距离 |
| std/var |
标准差/方差 |
| cumsum/cumprod |
累加/累乘 |
假设输入的形状是(m, n, k)
- 如果指定dim=0,输出的形状就是(1, n, k)或者(n, k)
- 如果指定dim=1,输出的形状就是(m, 1, k)或者(m, k)
- 如果指定dim=2,输出的形状就是(m, n, 1)或者(m, n)
size中是否有"1",取决于参数keepdim,keepdim=True会保留维度1。注意,以上只是经验总结,并非所有函数都符合这种形状变化方式,如cumsum。
b = t.ones(2, 3)
b.sum(dim = 0, keepdim=True)
output:
tensor([[2., 2., 2.]])
b.sum(dim=0, keepdim=False)
output:
tensor([2., 2., 2.])
b.sum(dim=1)
output:
tensor([3., 3.])
a = t.arange(0, 6).view(2, 3)
print(a)
a.cumsum(dim=1)
output:
tensor([3., 3.])
|
比较
比较函数中有一些是逐元素比较,操作类似于逐元素操作,还有一些则类似于归并操作。常用比较函数如表所示。
| 函数 |
功能 |
| gt/lt/ge/le/eq/ne |
大于/小于/大于等于/小于等于/等于/不等 |
| topk |
最大的k个数 |
| sort |
排序 |
| max/min |
比较两个tensor最大最小值 |
表中第一行的比较操作已经实现了运算符重载,因此可以使用a>=b、a>b、a!=b、a==b,其返回结果是一个ByteTensor,可用来选取元素。max/min这两个操作比较特殊,以max来说,它有以下三种使用情况:
- t.max(tensor):返回tensor中最大的一个数
- t.max(tensor,dim):指定维上最大的数,返回tensor和下标
- t.max(tensor1, tensor2): 比较两个tensor相比较大的元素
至于比较一个tensor和一个数,可以使用clamp函数。下面举例说明。
a = t.linspace(0, 15, 6).view(2, 3)
output:
0 3 6
9 12 15
[torch.FloatTensor of size 2x3]
b = t.linspace(15, 0, 6).view(2, 3)
output:
tensor([[15., 12., 9.],
[ 6., 3., 0.]])
|
a>b
output:
tensor([[False, False, False],
[ True, True, True]])
|
a[a>b]
output:
tensor([ 9., 12., 15.])
|
t.max(a)
output:
tensor(15.)
|
t.max(b, dim=1)
output:
torch.return_types.max(
values=tensor([15., 6.]),
indices=tensor([0, 0]))
|
t.clamp(a, min=10)
output:
tensor([[10., 10., 10.],
[10., 12., 15.]])
|
线性代数
PyTorch的线性函数主要封装了Blas和Lapack,其用法和接口都与之类似。常用的线性代数函数如表3-7所示。
表3-7: 常用的线性代数函数
| 函数 |
功能 |
| trace |
对角线元素之和(矩阵的迹) |
| diag |
对角线元素 |
| triu/tril |
矩阵的上三角/下三角,可指定偏移量 |
| mm/bmm |
矩阵乘法,batch的矩阵乘法 |
| addmm/addbmm/addmv/addr/badbmm… |
矩阵运算 |
| t |
转置 |
| dot/cross |
内积/外积 |
| inverse |
求逆矩阵 |
| svd |
奇异值分解 |
具体使用说明请参见官方文档[^3],需要注意的是,矩阵的转置会导致存储空间不连续,需调用它的.contiguous方法将其转为连续。
b = a.t()
b.is_contiguous()
output:
False
b.contiguous()
output:
0 9
3 12
6 15
[torch.FloatTensor of size 3x2]
|
Tensor和Numpy
Tensor和Numpy数组之间具有很高的相似性,彼此之间的互操作也非常简单高效。需要注意的是,Numpy和Tensor共享内存。由于Numpy历史悠久,支持丰富的操作,所以当遇到Tensor不支持的操作时,可先转成Numpy数组,处理后再转回tensor,其转换开销很小。
import numpy as np
a = np.ones([2, 3],dtype=np.float32)
b = t.from_numpy(a)
b = t.Tensor(a)
a[0, 1]=100
c = b.numpy()
|
- 注意: 当numpy的数据类型和Tensor的类型不一样的时候,数据会被复制,不会共享内存。
广播法则(broadcast)是科学运算中经常使用的一个技巧,它在快速执行向量化的同时不会占用额外的内存/显存。
Numpy的广播法则定义如下:
- 让所有输入数组都向其中shape最长的数组看齐,shape中不足的部分通过在前面加1补齐
- 两个数组要么在某一个维度的长度一致,要么其中一个为1,否则不能计算
- 当输入数组的某个维度的长度为1时,计算时沿此维度复制扩充成一样的形状
PyTorch当前已经支持了自动广播法则,但是笔者还是建议读者通过以下两个函数的组合手动实现广播法则,这样更直观,更不易出错:
unsqueeze或者view:为数据某一维的形状补1,实现法则1expand或者expand_as,重复数组,实现法则3;该操作不会复制数组,所以不会占用额外的空间。
注意,repeat实现与expand相类似的功能,但是repeat会把相同数据复制多份,因此会占用额外的空间。
a = t.ones(3, 2)
b = t.zeros(2, 3,1)
a+b
|
a.unsqueeze(0).expand(2, 3, 2) + b.expand(2,3,2)
|
e = a.unsqueeze(0).expand(10000000000000, 3,2)
|
内部结构
tensor的数据结构如图所示。tensor分为头信息区(Tensor)和存储区(Storage),信息区主要保存着tensor的形状(size)、步长(stride)、数据类型(type)等信息,而真正的数据则保存成连续数组。由于数据动辄成千上万,因此信息区元素占用内存较少,主要内存占用则取决于tensor中元素的数目,也即存储区的大小。
一般来说一个tensor有着与之相对应的storage, storage是在data之上封装的接口,便于使用,而不同tensor的头信息一般不同,但却可能使用相同的数据。下面看两个例子。
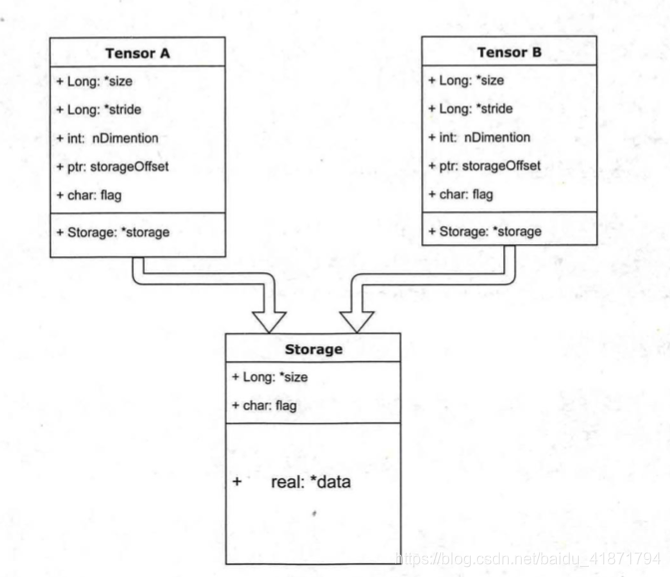
- 绝大多数操作并不修改tensor的数据,而只是修改了tensor的头信息。这种做法更节省内存,同时提升了处理速度。在使用中需要注意。
此外有些操作会导致tensor不连续,这时需调用tensor.contiguous方法将它们变成连续的数据,该方法会使数据复制一份,不再与原来的数据共享storage。
其它有关Tensor的话题
持久化
- Tensor的保存和加载十分的简单,使用t.save和t.load即可完成相应的功能。在save/load时可指定使用的
pickle模块,在load时还可将GPU的tensor映射到CPU或其它GPU上。
if t.cuda.is_available():
a = a.cuda(1)
t.save(a,'a.pth')
b = t.load('a.pth')
c = t.load('a.pth', map_location=lambda storage, loc: storage)
d = t.load('a.pth', map_location={'cuda:1':'cuda:0'})
|
向量化
向量化计算是一种特殊的并行计算方式,相对于一般程序在同一时间只执行一个操作的方式,它可在同一时间执行多个操作,通常是对不同的数据执行同样的一个或一批指令,或者说把指令应用于一个数组/向量上。向量化可极大提高科学运算的效率,Python本身是一门高级语言,使用很方便,但这也意味着很多操作很低效,尤其是for循环。在科学计算程序中应当极力避免使用Python原生的for循环。
def for_loop_add(x, y):
result = []
for i,j in zip(x, y):
result.append(i + j)
return t.Tensor(result)
|
x = t.zeros(100)
y = t.ones(100)
%timeit -n 10 for_loop_add(x, y)
%timeit -n 10 x + y
|
可见二者有超过40倍的速度差距,因此在实际使用中应尽量调用内建函数(buildin-function),这些函数底层由C/C++实现,能通过执行底层优化实现高效计算。因此在平时写代码时,就应养成向量化的思维习惯。
此外还有以下几点需要注意:
- 大多数
t.function都有一个参数out,这时候产生的结果将保存在out指定tensor之中。
t.set_num_threads可以设置PyTorch进行CPU多线程并行计算时候所占用的线程数,这个可以用来限制PyTorch所占用的CPU数目。t.set_printoptions可以用来设置打印tensor时的数值精度和格式。
下面举例说明。
a = t.arange(0, 20000000)
print(a[-1], a[-2])
b = t.LongTensor()
t.arange(0, 200000, out=b)
a = t.randn(2,3)
t.set_printoptions(precision=10)
|
线性回归
线性回归是机器学习入门知识,应用十分广泛。线性回归利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的,其表达形式为y=wx+b+e,e为误差服从均值为0的正态分布。首先让我们来确认线性回归的损失函数:
loss=i∑N21(yi−(wxi+b))2
然后利用随机梯度下降法更新参数w和b来最小化损失函数,最终学得w和b的数值。
import torch as t
%matplotlib inline
from matplotlib import pyplot as plt
from IPython import display
t.manual_seed(1000)
def get_fake_data(batch_size=8):
''' 产生随机数据:y=x*2+3,加上了一些噪声'''
x = t.rand(batch_size, 1) * 20
y = x * 2 + (1 + t.randn(batch_size, 1))*3
return x, y
x, y = get_fake_data()
plt.scatter(x.squeeze().numpy(), y.squeeze().numpy())
w = t.rand(1, 1).float()
b = t.zeros(1, 1).float()
lr =0.001
for ii in range(20000):
x, y = get_fake_data()
x = x.float()
y = y.float()
y_pred = x.mm(w).float() + b.expand_as(y).float()
loss = 0.5 * (y_pred - y) ** 2
loss = loss.sum()
dloss = 1
dy_pred = dloss * (y_pred - y)
dw = x.t().mm(dy_pred)
db = dy_pred.sum()
w.sub_(lr * dw)
b.sub_(lr * db)
if ii%1000 ==0:
display.clear_output(wait=True)
x = t.arange(0, 20).view(-1, 1).float()
y = x.mm(w) + b.expand_as(x)
plt.plot(x.numpy(), y.numpy())
x2, y2 = get_fake_data(batch_size=20)
plt.scatter(x2.numpy(), y2.numpy())
plt.xlim(0, 20)
plt.ylim(0, 41)
plt.show()
plt.pause(0.5)
print(w.squeeze()[0], b.squeeze()[0])
|







