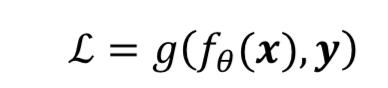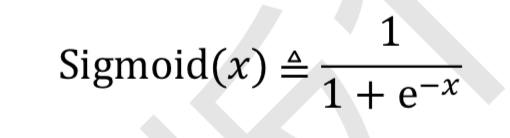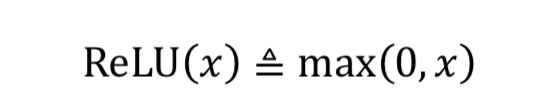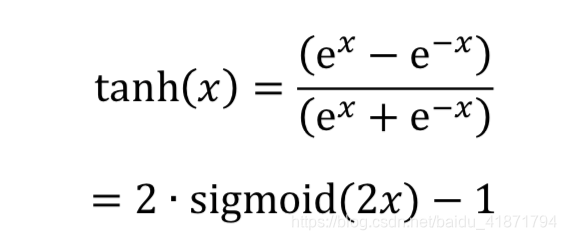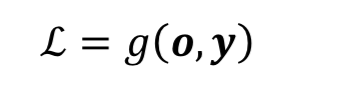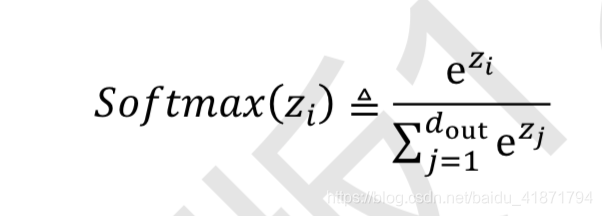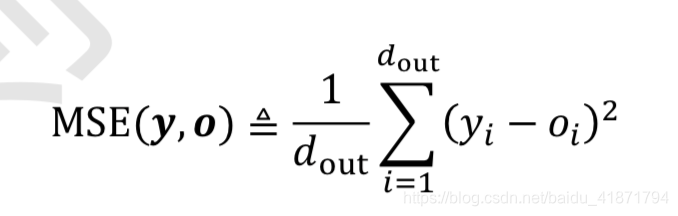使用Tensorflow2.0构建简单的神经网络

全连接层

在这里插入图片描述

𝑾矩阵叫做全连接层的权值矩阵，𝒃向量叫做全连接层的偏置向量

张量方式实现

定义好权值张量𝑾和偏置张量𝒃，并利用 TensorFlow 提供的批量矩阵相乘函数 tf.matmul()即可完成网络层的计算。

# 创建W,b张量
x = tf.random.normal([2,784])
w1 = tf.Variable(tf.random.truncated_normal([784, 256], stddev=0.1)) 
b1 = tf.Variable(tf.zeros([256]))
o1 = tf.matmul(x,w1) + b1 # 线性变换
o1 = tf.nn.relu(o1) # 激活函数
<tf.Tensor: id=31, shape=(2, 256), dtype=float32, numpy= array([[ 1.51279330e+00, 2.36286330e+00, 8.16453278e-01,1.80338228e+00, 4.58602428e+00, 2.54454136e+00,...

层方式实现

layers.Dense(units, activation)，通过 layer.Dense 类，只需要指定输出节点数 Units 和激活函数类型 activation 即可
输入节点数会根据第一次运算时的输入 shape 确定，同时根据输入、输出节点数自动创建并初始化权值张量𝑾和偏置张量𝒃，因此在新建类 Dense 实例时，并不会立即创建权值张量𝑾和偏置张量𝒃，而是需要调用 build 函数或者直接进行一次前向计算，才能完成网络参数的创建。

x = tf.random.normal([4,28*28])
from tensorflow.keras import layers # 导入层模块
# 创建全连接层，指定输出节点数和激活函数
fc = layers.Dense(512, activation=tf.nn.relu)
h1 = fc(x) # 通过 fc 类实例完成一次全连接层的计算，返回输出张量
<tf.Tensor: id=72, shape=(4, 512), dtype=float32, numpy= array([[0.63339347, 0.21663809, 0. , ..., 1.7361937 , 0.39962345,2.4346168 ],...

fc.kernel # 获取 Dense 类的权值矩阵
fc.bias # 获取 Dense 类的偏置向量
fc.trainable_variables # # 返回待优化参数列表 需要梯度更新的参数
fc.variables # 返回所有参数列表

神经网络

通过堆叠网络层可以实现一个复杂的神经网络。
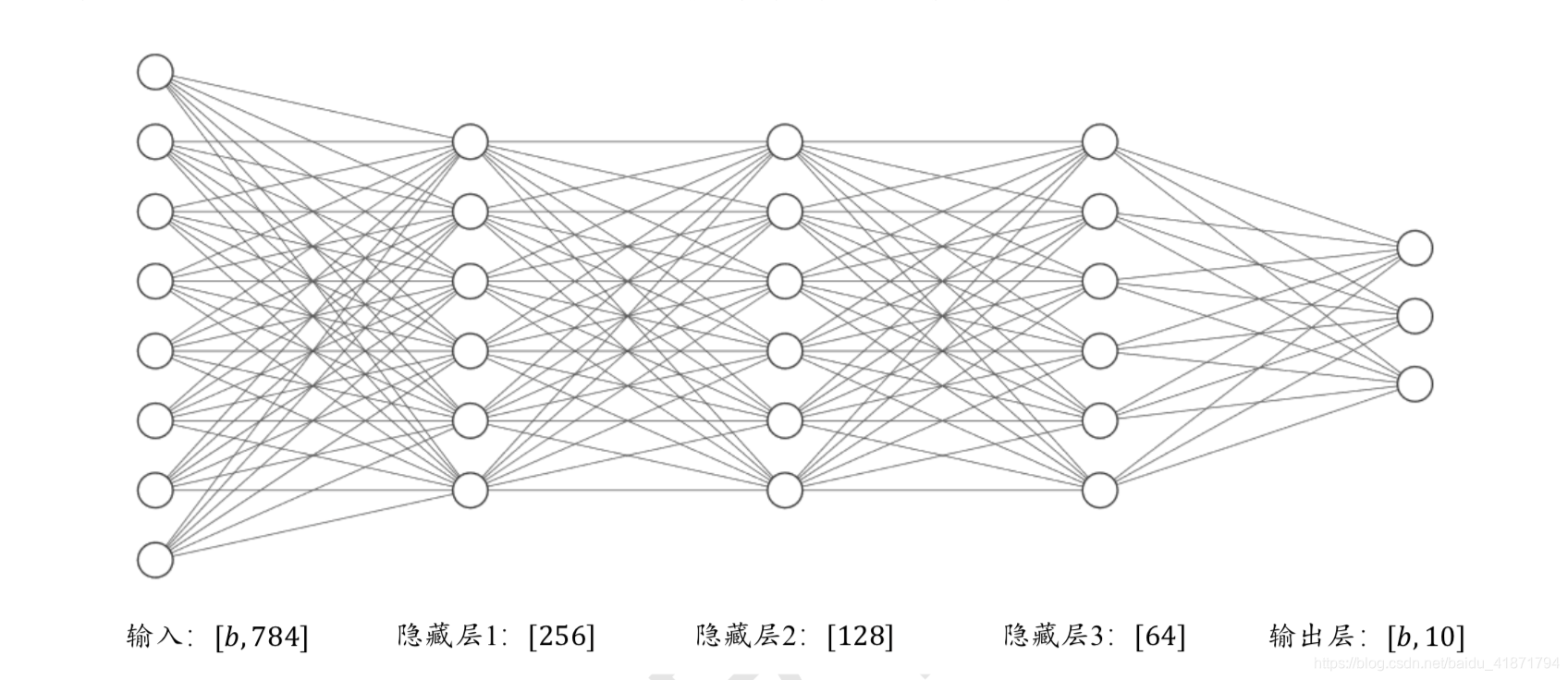
在这里插入图片描述

张量方式实现

# 隐藏层1张量
w1 = tf.Variable(tf.random.truncated_normal([784, 256], stddev=0.1))
b1 = tf.Variable(tf.zeros([256]))
# 隐藏层2张量
w2 = tf.Variable(tf.random.truncated_normal([256, 128], stddev=0.1)) b2 = tf.Variable(tf.zeros([128]))
# 隐藏层3张量
w3 = tf.Variable(tf.random.truncated_normal([128, 64], stddev=0.1)) b3 = tf.Variable(tf.zeros([64]))
# 输出层张量
w4 = tf.Variable(tf.random.truncated_normal([64, 10], stddev=0.1))
b4 = tf.Variable(tf.zeros([10]))

在计算时，只需要按照网络层的顺序，将上一层的输出作为当前层的输入即可，重复直至最后一层，并将输出层的输出作为网络的输出。
在使用 TensorFlow 自动求导功能计算梯度时，需要将前向计算过程放置在 tf.GradientTape()环境中，从而利用 GradientTape 对象的 gradient()方法自动求解参数的梯度，并利用 optimizers 对象更新参数。

with tf.GradientTape() as tape: # 梯度记录器
	# x: [b, 28*28]
	# 隐藏层 1 前向计算，[b, 28*28] => [b, 256]
	h1 = x@w1 + tf.broadcast_to(b1, [x.shape[0], 256]) h1 = tf.nn.relu(h1)
	# 隐藏层 2 前向计算，[b, 256] => [b, 128]
	h2 = h1@w2 + b2
	h2 = tf.nn.relu(h2)
	# 隐藏层 3 前向计算，[b, 128] => [b, 64] h3 = h2@w3 + b3
	h3 = tf.nn.relu(h3)
	# 输出层前向计算，[b, 64] => [b, 10] h4 = h3@w4 + b4

层方式实现

首先新建各个网络层类，并指定各层的激活函数类型:

# 导入常用网络层layers
from tensorflow.keras import layers,Sequential
fc1 = layers.Dense(256, activation=tf.nn.relu) # 隐藏层1 
fc2 = layers.Dense(128, activation=tf.nn.relu) # 隐藏层2
fc3 = layers.Dense(64, activation=tf.nn.relu) # 隐藏层3 
fc4 = layers.Dense(10, activation=None) # 输出层

在前向计算时，依序通过各个网络层即可。

x = tf.random.normal([4,28*28]) 
h1 = fc1(x) # 通过隐藏层 1 得到输出 
h2 = fc2(h1) # 通过隐藏层 2 得到输出
h3 = fc3(h2) # 通过隐藏层 3 得到输出 
h4 = fc4(h3) # 通过输出层得到网络输出

也可以通过 Sequential 容器封装成一个网络大类对象，调用大类的前向计算函数一次即可完成所有层的前向计算

# 导入Sequential容器
from tensorflow.keras import layers,Sequential
# 通过Sequential容器封装为一个网络类 
model = Sequential([
	layers.Dense(256, activation=tf.nn.relu) , # 创建隐藏层 1
	layers.Dense(128, activation=tf.nn.relu) , # 创建隐藏层 2 
	layers.Dense(64, activation=tf.nn.relu) , # 创建隐藏层 3
	layers.Dense(10, activation=None) , # 创建输出层
	])
 out = model(x) # 前向计算得到输出

优化目标

前向传播的最后一步就是完成误差的计算。

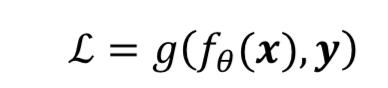
激活函数

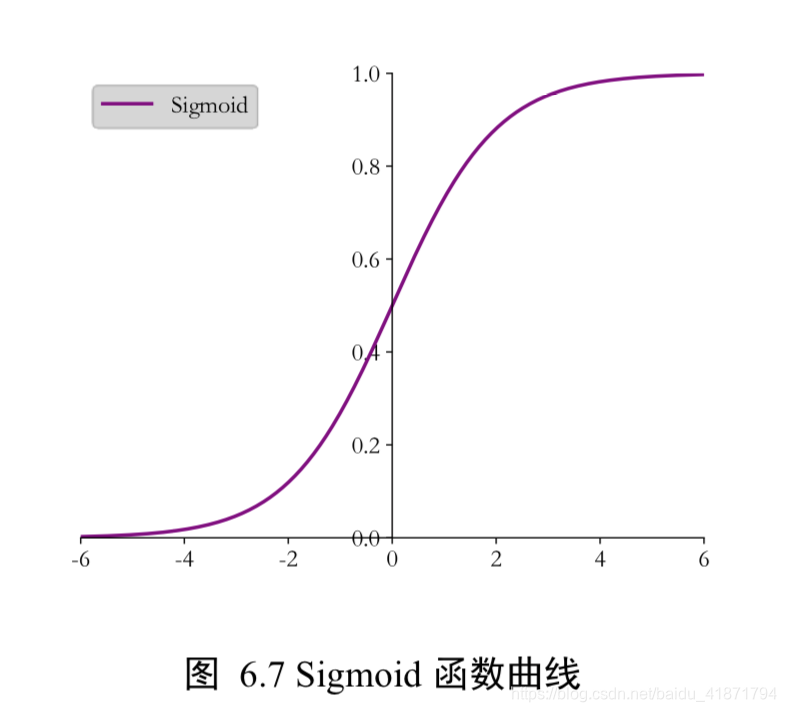
Sigmoid（Logistic 函数）

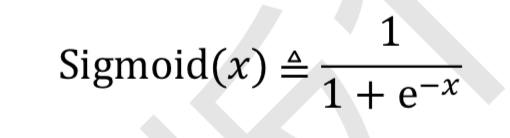
在这里插入图片描述

概率分布 (0,1)区间的输出和概率的分布范围[0,1]契合，可以通过 Sigmoid 函数将输出转译为概率输出
信号强度一般可以将 0~1 理解为某种信号的强度，如像素的颜色强度，1 代表当前通道颜色最强，0 代表当前通道无颜色;抑或代表门控值(Gate)的强度，1 代表当前门控全部开放，0 代表门控关闭

x = tf.linspace(-6.,6.,10) # 构造-6~6 的输入向量
tf.nn.sigmoid(x) # 通过 Sigmoid 函数

Sigmoid 函数在输入值较大或较小时容易出现梯度值接近于 0 的现象，称为梯度消失。

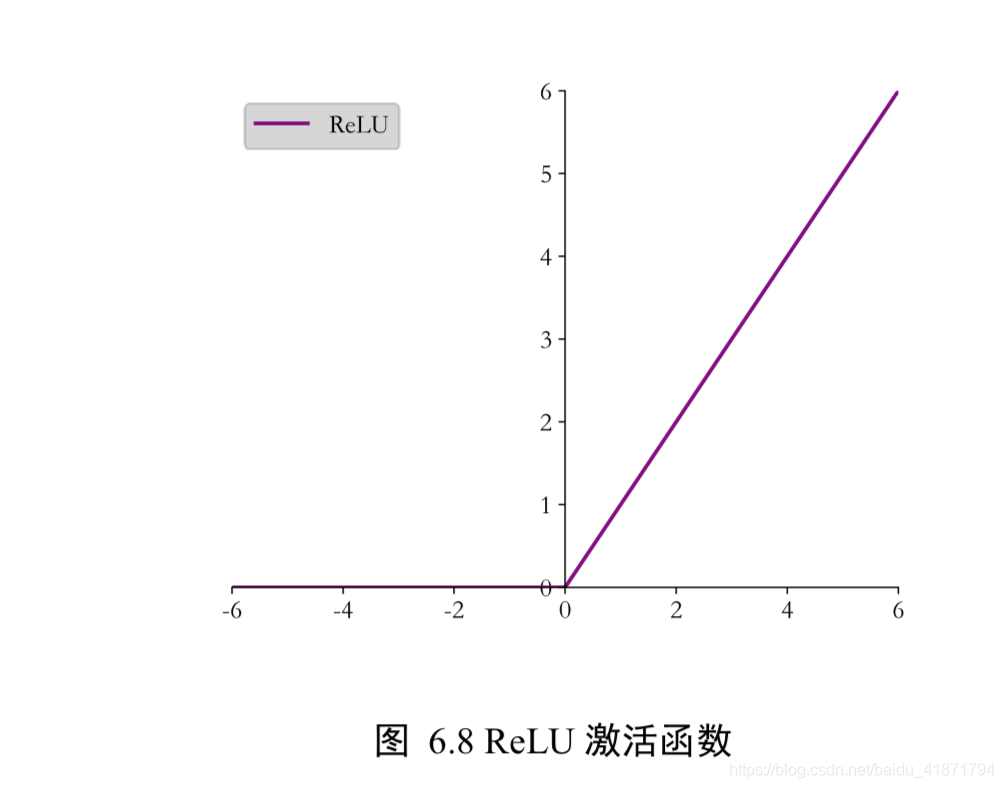
ReLU

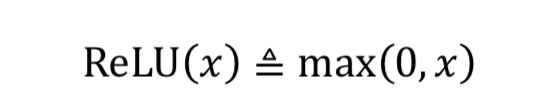
在这里插入图片描述

tf.nn.relu(x) # 通过 ReLU 激活函数

LeakyReLU

ReLU 函数在𝑥 < 0时导数值恒为 0，也可能会造成梯度弥散现象，所以提出LeakyReLU。

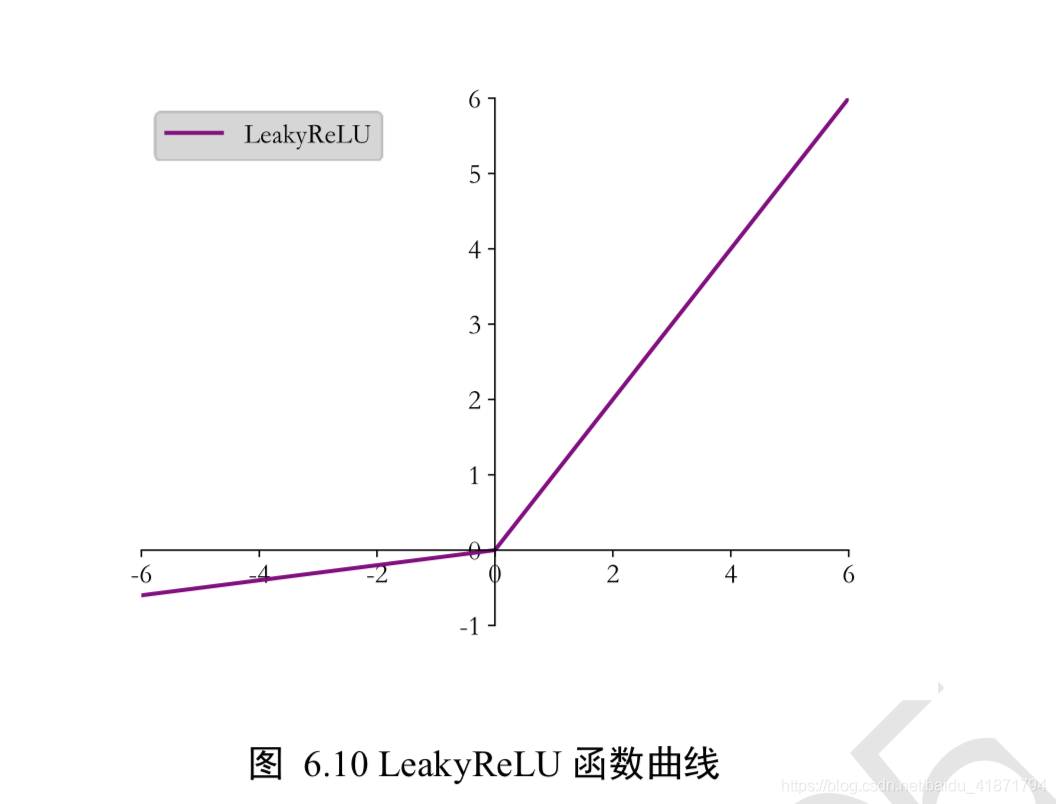
在这里插入图片描述

tf.nn.leaky_relu(x, alpha=0.1) # 通过 LeakyReLU 激活函数

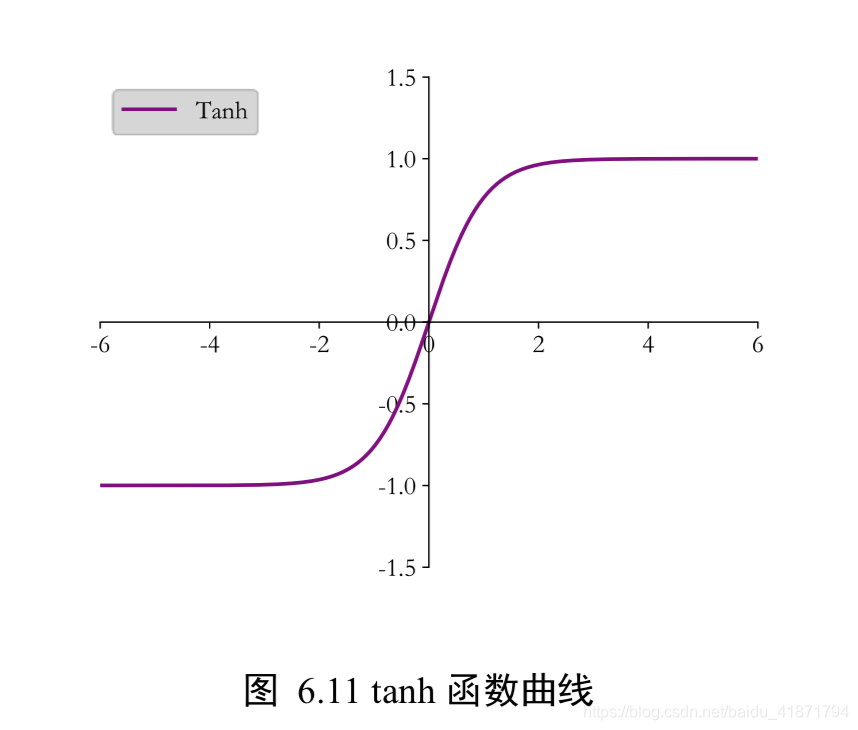
Tanh

Tanh 函数能够将𝑥 ∈ 𝑅的输入“压缩”到(−1,1)区间。
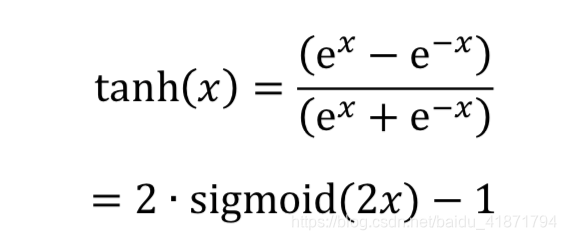
在这里插入图片描述

tf.nn.tanh(x) # 通过 tanh 激活函数

输出层的设计

𝑜𝑖 ∈ 𝑅𝑑 输出属于整个实数空间，或者某段普通的实数空间，比如函数值趋势的预测，年龄的预测问题等。
𝑜𝑖 ∈ [0,1] 输出值特别地落在[0, 1]的区间，如图片生成，图片像素值一般用[0, 1]区间的值表示;或者二分类问题的概率，如硬币正反面的概率预测问题。
𝑜𝑖 ∈ [0, 1], 𝑖 𝑜𝑖 = 1 输出值落在[0, 1]的区间，并且所有输出值之和为 1，见的如多分类问题，如 MNIST 手写数字图片识别，图片属于 10 个类别的概率之和应为 1。
𝑜𝑖 ∈ [−1, 1] 输出值在[-1, 1]之间

普通实数空间

正弦函数曲线预测、年龄的预测、股票走势的预测
输出层可以不加激活函数。误差的计算直接基于最后一层的输出𝒐和真实值𝒚进行计算

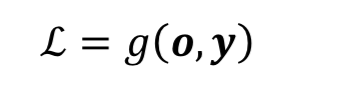
𝑔代表了某个具体的误差计算函数，例如 MSE 等。

[0, 1]区间

输出值属于[0, 1]区间也比较常见，比如图片的生成、二分类问题等。在机器学习中，一般会将图片的像素值归一化到[0,1]区间，如果直接使用输出层的值，像素的值范围会分布在整个实数空间。为了让像素的值范围映射到[0,1]的有效实数空间，需要在输出层后添加某个合适的激活函数𝜎，其中 Sigmoid 函数刚好具有此功能。

[0,1]区间，和为 1

考虑多分类问题中的样本只可能属于所有类别中的某一种，因此满足所有类别概率之和为 1
在输出层添加 Softmax 函数实现
通过 tf.nn.softmax 实现 Softmax 函数

z = tf.constant([2.,1.,0.1])
tf.nn.softmax(z) # 通过 Softmax 函数

通过类 layers.Softmax(axis=-1) 可以方便添加 Softmax 层，其中 axis 参数指定需要进行计算的维度
Softmax 与交叉熵损失函数同时实现，tf.keras.losses.categorical_crossentropy(y_true, y_pred, from_logits=False)，其中 y_true 代表了 One-hot 编码后的真实标签，y_pred 表示网络的预测值，当 from_logits 设置为 True 时， y_pred 表示须为未经过 Softmax 函数的变量 z;当 from_logits 设置为 False 时，y_pred 表示为经过 Softmax 函数的输出。

z = tf.random.normal([2,10]) # 构造输出层的输出
y_onehot = tf.constant([1,3]) # 构造真实值
y_onehot = tf.one_hot(y_onehot, depth=10) # one-hot编码
# 输出层未使用 Softmax 函数，故 from_logits 设置为 True
# 这样 categorical_crossentropy 函数在计算损失函数前，会先内部调用 Softmax 函数 loss = keras.losses.categorical_crossentropy(y_onehot,z,from_logits=True)
loss = tf.reduce_mean(loss) # 计算平均交叉熵损失 loss

利用 losses.CategoricalCrossentropy(from_logits)类方式同时实现 Softmax 与交叉熵损失函数的计算

# 创建 Softmax 与交叉熵计算类，输出层的输出 z 未使用 softmax 
criteon = keras.losses.CategoricalCrossentropy(from_logits=True) 
loss = criteon(y_onehot,z) # 计算损失
loss

[-1, 1]

如果希望输出值的范围分布在(−1, 1)区间，可以简单地使用 tanh 激活函数

x = tf.linspace(-6.,6.,10) 
tf.tanh(x) # tanh激活函数

误差计算

在搭建完模型结构后，下一步就是选择合适的误差函数来计算误差。常见的误差函数有均方差、交叉熵、KL 散度、Hinge Loss 函数等。
均方差函数主要用于回归问题，交叉熵函数主要用于分类问题。

均方差误差函数

均方差(Mean Squared Error，简称 MSE)误差函数把输出向量和真实向量映射到笛卡尔坐标系的两个点上，通过计算这两个点之间的欧式距离(准确地说是欧式距离的平方)来衡量两个向量之间的差距:
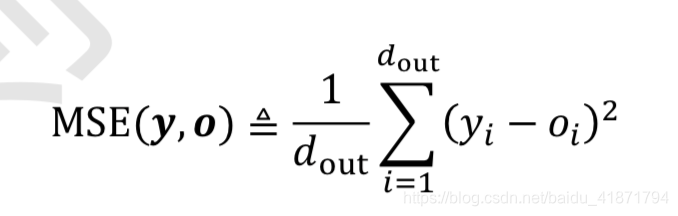
在这里插入图片描述

使用函数方式实现 MSE 计算

o = tf.random.normal([2,10]) # 构造网络输出 
y_onehot = tf.constant([1,3]) # 构造真实值
y_onehot = tf.one_hot(y_onehot, depth=10)
loss = keras.losses.MSE(y_onehot, o) # 计算均方差 loss
loss = tf.reduce_mean(loss) # 计算 batch 均方差 MSE 函数返回的是每个样本的均方差，需要在样本维度上再次平均来获 得平均样本的均方差

通过层方式实现，对应的类为 keras.losses.MeanSquaredError()，和其他层的类一样，调用__call__函数即可完成前向计算

# 创建MSE类
criteon = keras.losses.MeanSquaredError() 
loss = criteon(y_onehot,o) # 计算 batch 均方差

交叉熵误差函数

熵：代表系统的混乱程度，熵越大代表不确定性越大，信息量越大。

汽车油耗预测实战

采用 Auto MPG 数据集，它记录了各种汽车效能指标与气缸数、重量、马力等其它因子的真实数据

#%%
from __future__ import absolute_import, division, print_function, unicode_literals

import pathlib
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'


import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
 
import tensorflow as tf

from tensorflow import keras
from tensorflow.keras import layers, losses

print(tf.__version__)


# 在线下载汽车效能数据集
dataset_path = keras.utils.get_file("auto-mpg.data", "http://archive.ics.uci.edu/ml/machine-learning-databases/auto-mpg/auto-mpg.data")

# 效能（公里数每加仑），气缸数，排量，马力，重量
# 加速度，型号年份，产地
column_names = ['MPG','Cylinders','Displacement','Horsepower','Weight',
                'Acceleration', 'Model Year', 'Origin']
raw_dataset = pd.read_csv(dataset_path, names=column_names,
                      na_values = "?", comment='\t',
                      sep=" ", skipinitialspace=True)

dataset = raw_dataset.copy()
# 查看部分数据
dataset.tail()
dataset.head()
dataset
#%%


#%%

# 统计空白数据,并清除
dataset.isna().sum()
dataset = dataset.dropna()
dataset.isna().sum()
dataset
#%%

# 处理类别型数据，其中origin列代表了类别1,2,3,分布代表产地：美国、欧洲、日本
# 其弹出这一列
origin = dataset.pop('Origin')
# 根据origin列来写入新列
dataset['USA'] = (origin == 1)*1.0
dataset['Europe'] = (origin == 2)*1.0
dataset['Japan'] = (origin == 3)*1.0
dataset.tail()


# 切分为训练集和测试集
train_dataset = dataset.sample(frac=0.8,random_state=0)
test_dataset = dataset.drop(train_dataset.index) 


#%% 统计数据
sns.pairplot(train_dataset[["Cylinders", "Displacement", "Weight", "MPG"]], 
diag_kind="kde")
#%%
# 查看训练集的输入X的统计数据
train_stats = train_dataset.describe()
train_stats.pop("MPG")
train_stats = train_stats.transpose()
train_stats


# 移动MPG油耗效能这一列为真实标签Y
train_labels = train_dataset.pop('MPG')
test_labels = test_dataset.pop('MPG')


# 标准化数据
def norm(x):
  return (x - train_stats['mean']) / train_stats['std']
normed_train_data = norm(train_dataset)
normed_test_data = norm(test_dataset)
#%%

print(normed_train_data.shape,train_labels.shape) # 训练集共 314 行，输入特征长度为 9,标签用一个标量表示
print(normed_test_data.shape, test_labels.shape)  # 测试集共 78 行，输入特征长度为 9,标签用一个标量表示
#%%

class Network(keras.Model):
    # 回归网络
    def __init__(self):
        super(Network, self).__init__()
        # 创建3个全连接层
        self.fc1 = layers.Dense(64, activation='relu')
        self.fc2 = layers.Dense(64, activation='relu')
        self.fc3 = layers.Dense(1)

    def call(self, inputs, training=None, mask=None):
        # 依次通过3个全连接层
        x = self.fc1(inputs)
        x = self.fc2(x)
        x = self.fc3(x)

        return x

model = Network() # 创建网络类实例
# 通过 build 函数完成内部张量的创建，其中 None 为任意设置的 batch 数量，9 为输入特征长度
model.build(input_shape=(None, 9))
model.summary()   # 打印网络信息
optimizer = tf.keras.optimizers.RMSprop(0.001)  # 创建优化器，指定学习率
train_db = tf.data.Dataset.from_tensor_slices((normed_train_data.values, train_labels.values)) # 构建 Dataset 对象
train_db = train_db.shuffle(100).batch(32)  # 随机打散，批量化

# # 未训练时测试
# example_batch = normed_train_data[:10]
# example_result = model.predict(example_batch)
# example_result


train_mae_losses = []
test_mae_losses = []
for epoch in range(200):  # 200个Epoch
    for step, (x,y) in enumerate(train_db):  # 遍历一次训练集
        # 梯度记录器，训练时需要使用它
        with tf.GradientTape() as tape:
            out = model(x) # 通过网络获得输出
            loss = tf.reduce_mean(losses.MSE(y, out))  # 计算 MSE
            mae_loss = tf.reduce_mean(losses.MAE(y, out))  # 计算 MAE

        if step % 10 == 0 : # 间隔性地打印训练误差
            print(epoch, step, float(loss))
        # 计算梯度，并更新
        grads = tape.gradient(loss, model.trainable_variables)
        optimizer.apply_gradients(zip(grads, model.trainable_variables))

    train_mae_losses.append(float(mae_loss))
    out = model(tf.constant(normed_test_data.values))
    test_mae_losses.append(tf.reduce_mean(losses.MAE(test_labels, out)))


plt.figure()
plt.xlabel('Epoch')
plt.ylabel('MAE')
plt.plot(train_mae_losses,  label='Train')

plt.plot(test_mae_losses, label='Test')
plt.legend()
 
# plt.ylim([0,10])
plt.legend()
plt.savefig('auto.svg')
plt.show()